Summary
This page presents a highly simplistic simulation model that aims to make progress on the question of whether killing members of a food-limited animal population increases or decreases total long-run suffering. Because the model leaves out most real-world complications, its results shouldn't be taken at face value; rather, it should be viewed as one weak consideration among many when thinking about this issue. Additional and more complex models, combined with empirical data, could refine this analysis.
The results of the simulation are somewhat fragile in that they can change significantly with changes to just one input parameter. However, a general trend that often emerges is a U-shaped curve for average welfare as a function of how completely the animals are killed on a recurring basis. That is, (a) not killing or (b) regularly killing almost all animals is better than (c) regularly killing ~half of the animals. Regularly killing almost all the animals can cause less total suffering because in that scenario, the population remains low enough that you don't kill very many animals in absolute terms.
This conclusion can flip around if left-over accumulations of uneaten food slowly decay over time due to consumption by non-sentient organisms like bacteria. (If, as I do, one considers bacteria suffering to collectively matter somewhat as well, then the force of this point is reduced or eliminated.)
Many ways in which humans kill invertebrates, such as by walking on grass, kill only a small fraction of the total population. Relative to my model, these forms of killing plausibly cause net long-run harm compared against not killing at all.
Contents
Introduction
I generally encourage people to avoid walking on grass lawns because plant-covered ground contains large numbers of invertebrates that may be painfully maimed by footsteps. One common reply to my recommendation to "stay off the grass" is: "Won't the bugs die of something else later anyway? So does it matter if I'm the one who kills them?"
My usual response is: In a situation where total invertebrate populations are limited by the amount of food available, killing invertebrates now generally leaves around more food to be eaten by other bugs later. So killing bugs doesn't necessarily reduce total invertebrate populations in the long run, but it may increase the number of deaths per unit time.
Still, plausible counter-counterarguments can be made. For instance, one might claim that killing bugs before they can reproduce prevents a lot of babies from being born, most of whom will die not long after coming into existence.
A full accounting of the total suffering here is complex. This piece presents the simplest model of this situation that I could devise, in order to test these claims beyond surface-level heuristic arguments. This model is so simple that it shouldn't be interpreted as providing any definitive answers. But it illustrates the kinds of analyses that we could perform, with increasing levels of sophistication, in order to get slightly better intuition about the question at hand.
The model
 This model considers a barebones ecosystem consisting of a food supply and a single type of animal that eats it. For example, the food supply might be fungi, and the consumers might be springtails. I ignore other kinds of animals that might also eat the same food source. Predators, parasites, and pathogens of the consumer animals are treated as exogenous in that I account for the mortality they inflict but don't explicitly model their populations as changing.
This model considers a barebones ecosystem consisting of a food supply and a single type of animal that eats it. For example, the food supply might be fungi, and the consumers might be springtails. I ignore other kinds of animals that might also eat the same food source. Predators, parasites, and pathogens of the consumer animals are treated as exogenous in that I account for the mortality they inflict but don't explicitly model their populations as changing.
Discretize time t into days. t = 0 is the first day, t = 1 is the second day, etc. Assume that the food supply is created at a constant rate of F joules of food per day. For instance, every day, new grass blades and leaves fall to the ground and get covered with fungi, which the springtails can then eat. If all the food isn't eaten on a given day, it accumulates and is available to eat on subsequent days. However, some fraction B of the accumulated food gets eaten per day by organisms whose sentience will be ignored, such as bacteria. For instance, if B = 0.01, then 1% of the remaining food is lost each day. If you think bacteria/etc. are as morally significant per unit of metabolism as animals, then you might prefer to roughly approximate this value judgment by setting B = 0, which means that all left-over food gets eaten by sentient animals. (In fact, setting B = 0 runs the simulation as if there are no bacteria/etc. at all, so the results may not exactly match a simulation where bacteria/etc. do exist and matter morally, but I haven't written that latter simulation.)
Let NA(t) be the number of individual consumer animals with age of A days at time t. For simplicity, I start off the simulation with NA(0) = 1 for all ages A up to the max possible age, which I call Amax.
Individuals face the risk of death at any time due to predation, parasitism, disease, physical injury, etc. In particular, only a fraction P of individuals with age A reach age A+1, for all A. For example, if P = 0.99, then 1% of individuals die before the next day. If an individual gets lucky (or unlucky, depending on one's viewpoint) and survives all the way until age Amax, it dies that day.
Once individuals reach age AR (where AR ≤ Amax), they can begin reproducing. They produce H hatching offspring on each day of reproduction, and these offspring are assumed to hatch immediately for the sake of simplicity. Also for simplicity, I assume that all individuals can produce offspring, ignoring the difference between males and females. (If females typically hatch, say, 5 offspring per day, then you could set H as 5/2, which roughly approximates the per-parent hatching rate assuming males and females have similar survivorship trends.)
If individuals don't die, they need to consume some amount of food each day. The daily food requirement of an individual of age A is RA joules. If the individual doesn't get this food on a given day, it dies of starvation immediately. For simplicity, I model RA as being Aρ / ARρ (i.e., A raised to the ρ power, divided by the age when individuals can first reproduce raised to the ρ power) for some value of ρ, up until the animal matures at age AR, at which point RA is assumed to stay at ARρ / ARρ = 1. For instance, if ρ = 2/3 and AR = 30, then the daily food requirement of a 27-day-old animal would be 272/3 / 302/3 = 0.93, which is 9 times as much as the food requirement of a 1-day-old animal.
What if the population gets too big and there's not enough food to eat? In this case, some fraction of the individuals are assumed to eat their food requirements, while the rest eat nothing and starve. Starvation is assumed to be uniform across ages. For example, if 100 joules of food are required and there are only 50 joules available, then half of individuals at all ages die of starvation, while the other half eat the food and grow. As a result of food limitation, after initial population growth, the consumers will reach a relatively steady state of population size.
Let SA be the sentience of an individual of age A. In generally, SA should increase with bigger values of A, since adults generally have more developed brains than young offspring do. I model SA as Aσ / ARσ (i.e., A raised to the σ power, divided by the age when individuals can first reproduce raised to the σ power) for some value of σ, up until the animal matures at age AR, at which point SA is assumed to stay at ARσ / ARσ = 1.
L represents the net happiness or suffering that individuals experience during a day of life (relative to the sentience of the organism), and D represents the painfulness of dying (relative to the sentience of the organism). In other words, the moral (dis)value of a day of life of an individual with age A is SA * L, and the moral disvalue of its death at age A is SA * D. L can be positive or negative, while D is negative (or at most 0).
Finally, we need to model the process of killing some of the animals, such as by stepping on them. I'll assume that this causes a uniform mortality rate of M across all ages. For example, if we started with 8 individuals at age 0 and 4 individuals at age 1, and if M = 0.25, we would end up with 8 * (1-0.25) = 6 individuals at age 0 and 4 * (1-0.25) = 3 individuals at age 1. Let Dk represent the painfulness of dying due to being killed in this way. And suppose that this killing happens once every K days. For example, if a person walks on springtail-filled grass once a week, K = 7. K must be a positive integer so that it falls on one of the discrete time steps of the simulation.
If M is set very high—e.g., if it's set to 1, meaning that all animals are killed—then suffering would drop to 0 thereafter, since there would be no further breeding. However, the food source would still produce food, and in the real world, animals would still come back to eat it, eventually. Thus, the reported suffering values of this model would be wrong, since this model would assume the food never gets eaten. To avoid this problem, M can't be set higher than 0.95. But even at M = 0.95, if killing happens often enough, the population could be kept artificially low indefinitely, and food would keep accumulating indefinitely. This would also make the simulated suffering values too low. For this reason, I assume that killing events stop halfway through the simulation. For example if you run the simulation for T = 1000 days, killing stops after day 500, which gives the population a chance to recover and eat down the excess food. Finally, to prevent killing from driving population numbers down to basically 0 before killing stops at T/2, I assume that if the current number of individuals alive with a given age is less than 1 (NA < 1), then the number of individuals with that age will be spared from your killing this time around. (They will not, however, be spared from predation, starvation, or other "natural" causes of death.)
The above model is simulated in JavaScript over T total days. To see the code, view the source of this page and look for the calculate() function.
Below I show various metrics of the results, the most important being the average net hedonic experience per day, i.e., the sum over all individuals of happiness minus suffering, weighted by the sentience of each individual, added over all days of the simulation, divided by T.
In the simulation, I allow fractional numbers of animals, since all the equations work whether the number of animals is a fraction or a whole number. In reality, the numbers of animals involved would be many times what's simulated here, so using fractions isn't unrealistic. For instance, you could think of NA(t) as being the number of individuals with age A at time t measured in thousands, so that NA(t) = 0.05 would actually be 50 individuals.
Parameter settings
I set parameters in the following table loosely based on the biology of springtails. The end of this page explains in more detail the justification of some of the parameter settings. That said, this calculator is intended to work for a variety of possible inputs.
| Variable | Symbol | Value |
| Days to run simulation | T | |
| New food added per day | F | |
| Fraction of accumulated food lost per day to non-sentient organisms | B | |
| Max possible age (in days) | Amax | |
| Fraction of individuals surviving to next day | P | |
| Age (in days) when can begin reproducing | AR | |
| Hatching offspring created per day by a reproducer | H | |
| Food-intake exponent ρ for the relationship RA = Aρ / ARρ | ρ | |
| Sentience exponent σ for the relationship SA = Aσ / ARσ | σ | |
| Net happiness or suffering of a day of life (negative means suffering) | L | |
| Suffering from dying of natural causes | D | |
| Suffering from being killed by a human | Dk | |
| Mortality rate when a human causes death | M | |
| Days between human killings | K |
How suffering varies with killing intensity
The following graph shows the final value (at the end of the simulation) of the long-run average of welfare over time as a function of M, the fraction of individuals killed at each killing event.
(Remember that negative welfare numbers mean net suffering.)
Using my default parameters, there's a U-shaped curve where either killing no animals or killing almost all of them at each killing event is better than killing some but not all. Why is this? Why doesn't welfare just increase or just decrease with higher values of M? My guess is that when M is very high, the animal population is driven to a relatively small size until the killing stops. When the population is small, the repeated killing events don't kill very many animals in absolute terms. Hence, having a value of M close to 1 is sort of like having a value of M close to 0. In contrast, if M is around 0.3, the population remains reasonably large, so each killing event kills more total animals than if M were, say, 0.9.
- You can see the preceding point by starting with the default parameters and then setting D to 0 (leaving Dk at -1). Now, welfare is only tracking suffering from human-caused deaths. You can see that the shape of the graph is not dramatically changed relative to how it looked with the default parameters. In other words, there are actually fewer (sentience-weighted) human-caused deaths for values of M close to 1 than for values of M around 0.3.
- If you keep D at -1 and set Dk to 0, the trend is reversed: Welfare is highest for values of M around 0.3. Presumably this is because when humans kill animals, those animals are spared from dying naturally later on.
Unfortunately, this finding is somewhat sensitive to many of the input parameters, as you can see by playing around with them. In some cases, weirdness results if you change parameters in such a way that the population can't sustain itself over time, such as by lowering H. (You can see population size in the "Visualizing the dynamics" section of this piece below.) But even in cases where the population remains stable over time, you can get fairly different curves for "average daily welfare vs. M" depending on inputs. For example, increasing σ to 1 (i.e., making sentience linear in age up to age AR) turns the U-shaped curve into a curve that basically just increases with M.
The behavior of the curve with respect to the B parameter is intuitive. For instance, if B = 0.01, then the above graph increases for increasing values of M, i.e., killing reduces overall suffering. More killing means more of the food reserves get eliminated by non-sentient organisms, which means lower future populations of animals. And if, in addition to setting B = 0.01, we change L from its default of 0 to 0.1 (i.e., daily life is quite positive on balance for the animals), then more killing is welfare-reducing because loss of food to non-sentient organisms means fewer total animal-days of life exist.
How much long-run suffering is caused by how much direct-killing suffering?
Using the default parameters, killing animals (M > 0 but not near 1) increases total suffering somewhat. But presumably the long-run increase in suffering is less than what one might naively think just by looking at the process of killing, because killing may prevent some natural deaths from occurring later on. Using this model, we can make this point precise.
Using the value of M currently set, the reduction in long-run daily-average welfare due to killing, compared against no killing, is . You can see this in the previous graph as the difference between the welfare value at M = 0 and at the currently set value of M. Meanwhile, if we add up the total direct suffering caused by human killing during the simulation (i.e., the total painfulness of all human-caused deaths), the total has an absolute value of . The ratio of these two is / = , i.e., for every 1 unit of direct suffering caused by killing animals, this translates into a long-run increase in population-wide suffering of only units.
Visualizing the dynamics
To help visualize how the population dynamics work, below are a few charts, showing diagnostic variables over the first days of the simulation.
No human killing
First, let's see what things look like if M = 0, i.e., if humans don't kill any animals.
With human killing
Now, what happens if M is set at the value that you set it at?
Life-history information for springtails
This section gives more explanation of how I chose some of the default parameters.
ρ value
I didn't find information on the growth rate of springtails, but Lundy and Parrella (2015) offer the following growth curve for farmed crickets:
The top two curves seem to have faster-than-linear growth, maybe a bit less than quadratic or so? That said, growth is pretty slow until day ~15. Still, let's roughly approximate body mass m as a function of day t as m(t) = t2.
Keep in mind that body mass is not the same as food requirements. Food requirements come from metabolism and growth.
- If springtails follow Kleiber's law, then metabolism is m3/4. So if m(t) = t2, metabolism would be proportional to (t2)3/4 = t3/2.
- Food required for growth should be proportional to the rate of change of body mass, i.e., dm/dt = 2 * t.
Combining these considerations, we might expect food consumption as a function of time to be slightly more than linear. Of course, this is a very theoretical sketch of an argument that may be inaccurate in practice. Finally, we should keep in mind that these cricket growth curves are plausibly steeper than those of wild invertebrates, who don't necessarily have constant access to food and stable living conditions.
By the way, Maino and Kearney (2015) note in their "Introduction" that "It has long been suggested that insect growth is more closely characterized by exponential growth, with von Bertalanffy himself noting that insects could be classed as a unique metabolic and growth type that is closer to exponential [7]." (The authors go on to propose a more nuanced model.)
P, H, and Amax values
Choi et al. (2002) studied population dynamics of the Paronychiurus kimi springtaila under laboratory conditions. I'll extract approximations of P, H, and Amax from the following figure.
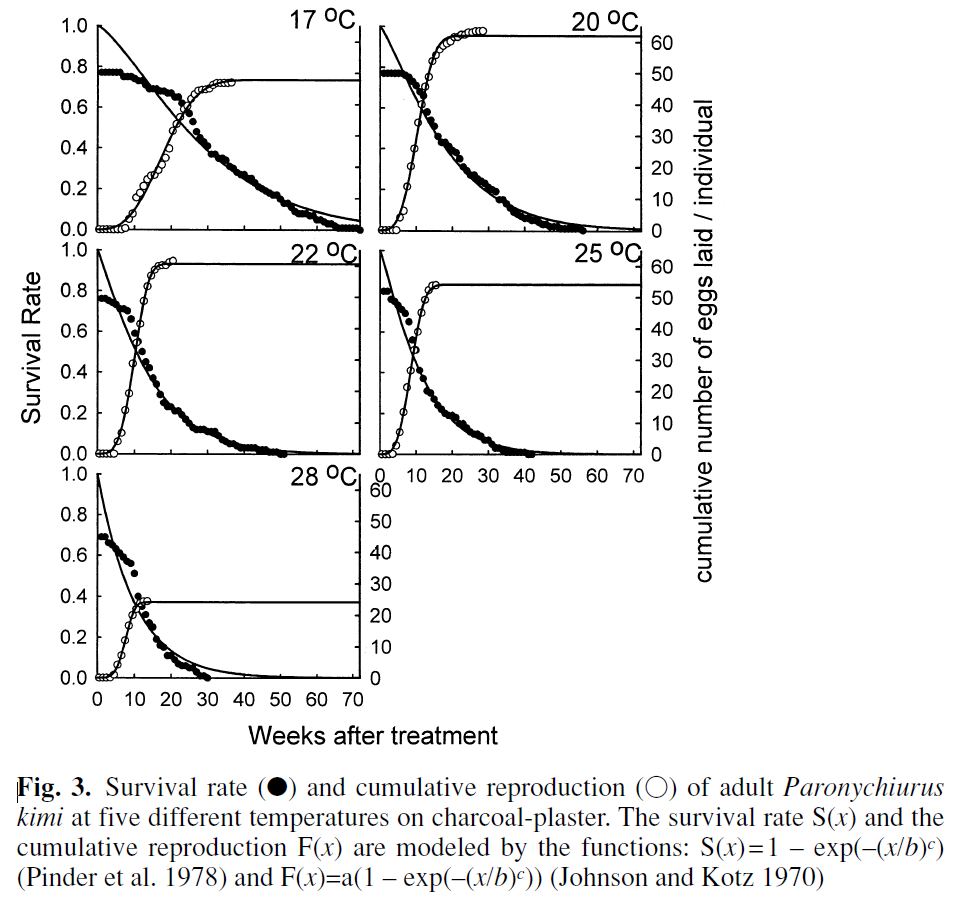
P value
The above figure shows survival of adults specifically, but my model (unrealistically) assumes a constant daily percentage survival rate of P for both juveniles and adults, so it's sufficient to estimate P from the adult numbers. It's not obvious which temperature's data to use, but let's go with the middle value: 22°C. Based on eyeballing the figure, it looks to me like survival hits 0.6 after around 9 weeks = 63 days. Solving P63 = 0.6 gives P = 0.99. This number seems fairly consistent with the rest of the graph. For instance, at 20 weeks = 140 days, we would expect survival to be 0.99140 = 0.24, which is pretty close to the actual value in the graph. At 30 weeks = 210 days, we would expect survival to be 0.99210 = 0.12, which is again quite close to the actual value.
However, these springtails were raised under favorable laboratory conditions, presumably free from predators and many other dangers. So actual survival rates in the wild are probably a fair amount worse. I don't have specific numbers on how much worse, so I just assumed that the actual value of P is 0.98, rather than 0.99.
Amax value
The survivorship curve for 22°C seems to drop off around 50 weeks, i.e., about a year. The exact value of Amax doesn't matter too much, and the only reason it's included at all is to speed up the calculations.
H value
The plateau of the "cumulative number of eggs laid / individual" curve in the above figure seems to be about ~61 for 22°C. Choi et al. (2002) clarify (p. 551) that this is actually "number of eggs laid per female", whereas my parameter is "number of eggs laid per male or female", so let's divide this in half: ~30 eggs per individual. In addition, Fig. 1 (p. 551) shows a "hatchability" of eggs of roughly 75%. So total hatching eggs per individual is probably around 30 * 0.75 = 23. My model (unrealistically) assumes a constant value for H, the number of hatching eggs laid per day per adult individual. Let E be the expected number of days of future life a springtail has ahead of it once that springtail has reached adulthood (i.e., has reached age AR). We require that E * H = 23, so H = 23/E. Below I'll show that E = 100, so that H = 0.23.
Define "adult_age" as the number of days for which a springtail has been an adult, i.e., adult_age is (springtail's age since birth) - AR. E is the expected value of adult_age. Abbreviate adult_age as z. Let S(z) be the fraction of adults surviving to an adult_age of z days. S(0) = 1. The fraction of adults that die with an adult_age between z and z+1 days is S(z) - S(z+1) for z ≥ 0. Hence, a discrete approximation of E is
= S(1) - S(2) + 2 * [S(2) - S(3)] + 3 * [S(3) - S(4)] + ...
= S(1) + S(2) + S(3) + ...
For the continuous version of E, let's first consider the inverse of the S(z) function: S-1(s), where s is a survivorship value. For example, S-1(0.5) gives the adult_age at which survivorship reaches 0.5. A fraction Δs of individuals die between adult_ages S-1(s) and S-1(s + Δs). For small values of Δs, this is approximately adult_age S-1(s). In total,
E = ∫01 S-1(s) ds.
Visually, we can see that this integral is computing the area under the S(a) curveb, so E also equals
which is a continuous version of the S(1) + S(2) + S(3) + ... expression. As before, let's approximate the survivorship curve at 22°C in Choi et al. (2002)'s Fig. 3 as
S(z) = 0.99z ≈ e-0.01 * z.
Then
E ≈ ∫0∞ e-0.01 * z dz = [ -100 * e-0.01 * z ]0∞ = (-100 * e-0.01 * ∞) - (-100 * e-0.01 * 0) = 100.
We could have gotten the same result by noting that the adult_age of death follows a geometric distribution with the daily death probability p = 0.01. The expected value of a geometric random variable is 1/p = 1/0.01 = 100.
AR value
This page says: "Springtails reproduce rapidly and a single life cycle may take just 3-5 weeks from hatching to maturity."
Choi et al. (2002) report that at 22°C, the juvenile development rate was 0.18 (based on my eyeballing of Fig. 2, p. 552), where "The developmental rate of P. kimi is defined as the reciprocal of the mean period (in weeks) to complete development" (p. 550). So it takes 1/0.18 = 5.6 weeks = 39 days to complete juvenile development.
Are invertebrate populations actually food-limited?
Using the default parameters of the above model, the simulation shows that excess food is eventually eaten down by the invertebrate population, i.e., that food is limiting on population size. But are invertebrate populations actually limited by food in reality?
Cuddington (2019) explains regarding herbivorous insects: "Competition is a very small factor in total juvenile mortality, and the vast majority of mortality events are caused by predators and parasitoids. The weather, intrinsic factors related to reproduction (egg viability) and plant defences also explained more mortality than competition." In a comment on Cuddington (2019), the article's author confirms that starvation represents "a lowish percent of total mortality."
Assuming the same trend holds for detritivores as herbivores, then I guess more realistic parameter settings for the above model should take the P parameter to be smaller, meaning that death by predation, parasitism, etc is more significant. For example, if you set P to 0.95, then you can see from the "Amount of left-over food (no human killing)" graph that food is no longer limiting, and excess food keeps accumulating over time. However, my model gives warnings when you set P this low. Allowing excess food to accumulate uneaten by the species being modeled here could mean that some other species of invertebrate would be eating it. Since my model only keeps track of the main invertebrate species under consideration, the model would fail to count the welfare of the other invertebrate species involved.
From a macroscopic perspective, we can see that heterotrophs collectively usually are food-limited because most of the waste organic matter on Earth gets eaten. If heterotrophs were limited by something besides food, then organic waste would keep accumulating. However, individual types of heterotrophs could be limited by other factors than food. For example, maybe invertebrate decomposers are generally not food-limited, and it's bacteria, fungi, and other non-invertebrates who are the food-limited decomposers?
It's also worth noting that competition for food isn't the only way in which invertebrates can limit one another's abundance. Cuddington (2019) explains: "meta-analyses consistently find evidence of negative effects of one insect herbivore species on another; however, the suggested mechanisms for this impact are predominantly indirect effects (e.g., inducing stronger plant defences and increasing predator populations). Direct lethal impacts caused by food shortages are considered less common." So even without food limitation, it could still be the case that killing some members of an herbivore population allows other herbivores to take their place to some extent.
Footnotes
- I couldn't find a picture of Paronychiurus kimi, but they're in the family Onychiuridae, just like the Protaphorura armata springtails in the image near the top of this essay. (back)
- This point can also be proved using a theorem by Charles-Ange Laisant.
In this proof, let "∞" stand for a huge but finite number, where S(∞) is basically 0.
Let W be the antiderivative of S. Then, using Laisant's theorem:
E = ∫01 S-1(s) ds = [ s * S-1(s) - (W o S-1)(s) ]01,
where by [ ]01 I mean (the expression inside the [ ] evaluated at s = 1) minus (the expression inside the [ ] evaluated at s = 0).
Note that S-1(1) = 0 (everyone is alive at adult_age 0). Hence, s * S-1(s) = 0 for both s = 0 and s = 1, since in either case, one factor in this product is 0. Thus, we're left with justE = [ -(W o S-1)(s) ]01 = (W o S-1)(0) - (W o S-1)(1).
S-1(0) = ∞ because the adult_age at which everyone dies is ∞. So we have
E = W( S-1(0) ) - W( S-1(1) ) = W(∞) - W(0) = [ W ]0∞ = ∫0∞ S(a) da,
where the last equality follows from the definition of W. QED. (back)