Summary
Phenomenal consciousness is not an ontologically fundamental feature of the universe; rather, it's something we attribute to physical systems when we take a "phenomenal stance" toward them. This piece outlines some general ways in which we might formalize our intuitions about which physical entities are conscious to what degrees. In particular, we can invoke many traditional theories of consciousness from the philosophy of mind, such as identity theory and functionalism, as frameworks for sentience attribution. Functionalism faces a problem of indeterminacy about what abstract computation a physical system is implementing, and one possible resolution is to weigh different interpretations based on their simplicity, reliability, counterfactual robustness, and other factors.
Contents
- Summary
- Introduction
- Building a sentience classifier
- A taxonomy of some approaches
- Computations are relative to interpretation
- Example: Particles "implementing" a Turing machine
- Representational arbitrariness in computer science
- Using many possible interpretations?
- Constraint satisfaction for interpretations
- Higher-level computations
- Interpretational relativity is not unique to functionalism
- Functionalism as a sliding scale among physicalist theories
- How much do we care about various traits?
- Summary of our classifier
- Optional: Personal history with this topic
- Appendix: Other implications of interpretational relativity of computations
- Acknowledgments
- Footnotes
Introduction
If we care about the welfare of others, we want to know what kinds of emotions others are experiencing and then assess whether those emotions are good or bad. We want to reduce bad emotions and maybe cause more good emotions.
But according to Type-A physicalism, emotions are not ontologically primitive properties of the universe. Rather, there is just physics, and emotions are concepts that we attribute to physical systems, in a similar way as "good" and "bad" are moral labels that we attribute to situations and actions.
By "physical system" I mean some subset of the universe. Typical examples include
- the brain of a specific South American pilot between 10:00 and 10:01 on a given date
- a particular aphid crawling on a particular leaf of lettuce
- the running of a web browser on some specific computer at some specific time
- a one-minute segment of a solar flare by a particular star in the Milky Way on a specific date.
How can we attribute emotions and welfare to physical systems? What criteria should we use? This piece explores a few options. The list of ideas is not exhaustive, and we could use several of these approaches in conjunction and then combine the resulting assessments together.
Building a sentience classifier
Our question is: For a given physical system, what kinds of emotion(s) is it experiencing and how good/bad are they? The answers will not be factual in any deep ontological sense, since emotions and moral valence are properties that we attribute to physics. Rather, we want an ethical theory of how to make these judgments.
An answer to this question will be a "sentience classifier", taking in descriptions of physical systems and outputting attributed emotion(s) and their valence(s). For instance, if we give this program the physics of your brain during a particularly joyful moment of your life, it should output, say,
- "joy", "elation"
- value = +100.
We humans already have sentience classifiers in our brains. The goal of developing a more explicit sentience classifier is to propose a more transparent and less chauvinist approach for attributing mental life to physical systems. Reflecting on how the classifier works may change our pre-existing, patchwork intuitions.
A taxonomy of some approaches
Sentience classifiers can be built based on theory, training examples, or both. A theoretical approach develops general ideas about sentience from abstract first principles. An approach using training examples takes existing instances of physical processes that are already felt to be sentient in various ways and fits the classifier to them.
The target output values for these training examples are made up according to subjective reports, preference tradeoffs, and/or the intuitions of the person building the classifier. For example, perhaps I think the processes in a person's brain while drowning for one minute have badness -50, and the processes in that person's brain while burning alive for one minute have badness -400. The classifier can also be used to refine one's intuitions. For example, if I naively thought that drowning was less bad than another manner of death, but I then discovered that the classifier predicted a very severe badness for drowning based on certain types of brain activity, I might revise my initial judgments.
The following table taxonomizes some classifier approaches based on what kind of match, if any, they check for against training data (columns) and what kinds of criteria are used in making the evaluation (rows). The table may be confusing, but I explain in more detail below.
| Trained (exact match) | Trained (fuzzy match) | Theory | |
| Physical traits | token identity | type identity | various physical criteria |
| Chauvinist functionalism | defined inputs/outputs, algorithm exactly matches a training example | defined inputs/outputs, algorithm has similarities to training examples | defined inputs/outputs, general functional criteria |
| Liberal functionalism | any inputs/outputs, algorithm exactly matches a training example | any inputs/outputs, algorithm has similarities to training examples | any inputs/outputs, general functional criteria |
| Pre-reflective intuitions, gut feelings, etc. | (this is roughly what we normally use) | use gut feelings as one component of the evaluation |
In this context, token physicalism essentially means a lookup-table classifier: Check if the input physical system is in the list of training examples, and if there's an exact match, return its labeled emotions and valences. In philosophy of mind, token physicalism typically carries metaphysical weight, postulating that mental events actually exist (Type-B physicalism) and are identical to specific brain events. Here I'm extracting the idea behind the theory without the ontological claim that consciousness is a real, definite thing. Needless to say, the judgments that token physicalism can make are limited to the training examples. If we provide the training examples using our own pre-theoretical judgments, then token physicalism ends up collapsing to our original intuitions.
Type identity is not just a lookup table but instead is more of a feature-based classifier. In philosophy of mind, the standard (though neurologically impoverished) example of a type-physicalist judgment is that X is in pain if and only if X has C-fiber firings. In other words, the presence of C-fiber firings is a (maximally powerful) input feature for the classification of pain. By matching on features of the input rather than the entire input, this approach can generalize beyond the training set. We developed the rule mapping from C-fibers to pain based on the data we gave the classifier, but now it can attribute pain to any creature with firing C-fibers. As with token physicalism, type physicalism usually coincides with a commitment to the metaphysical reality of mental states, but I'm appropriating it for my own purposes.
My distinction between "chauvinist" and "liberal" functionalism is based on Ned Block's "Troubles with Functionalism":
- Chauvinist functionalism requires that inputs and outputs be of a certain type (e.g., only neural firings can be inputs, and only movements by an animal's body parts can be outputs)
- Liberal functionalism allows inputs and outputs to be anything, so long as the logical structure of the computation remains preserved.
Exact-match versions of functionalism attribute sentience only to systems that instantiate an algorithm identical to the algorithm of some input training example. Fuzzy-match functionalism abstracts away higher-level ideas behind what a computation is doing, allowing for generalization beyond algorithms in the training set.
For example, if I am in the training set, exact-match functionalism would look for systems that are performing the exact computations my body is performing. Fuzzy-match functionalism would recognize that my body has many general kinds of operations, like speech, memory, planning, reinforcement learning, information broadcasting, avoidance of stimuli, crying out, and the like. It then pattern-matches other systems against these features and assesses sentience based on whether and how much these kinds of operations are present.
Suppose we took only my body as the training set. Here are examples of what kinds of things would then be considered sentient according to different forms of functionalism:
- Exact-match chauvinist functionalism would probably only classify as sentient my biological self and maybe some cyborg versions of myself. Due to chauvinism, the inputs must be, say, biological neurons, and the outputs must be, say, biological limb movements. The internal computations, however, can occur on any substrate—unlike token or type physicalism, which would require biological internals as well.
- Fuzzy-match chauvinist functionalism might attribute sentience to many animals, since they have biological inputs/outputs and have internal algorithms that resemble mine at a generic level, even though the exact computations aren't the same.
- Exact-match liberal functionalism would attribute sentience to not just cyborgs but full digital emulations of my body, since the restriction on the nature of the inputs and outputs would be lifted. It might also weakly attribute sentience to chance physical processes of a very abstract nature that happen to map properly onto my body's algorithms, including (with very low but nonzero probability) the economy of Bolivia, as Block discusses in his paper.
- Fuzzy-match liberal functionalism would attribute sentience to many systems—people, animals, computer programs, and maybe even crude physical processes—insofar as they contain instances of general kinds of algorithms in my brain.
My personal ethical inclinations identify most strongly with fuzzy-match liberal functionalism.
Computations are relative to interpretation
Physicalist views that directly map from physics to moral value are relatively simple to understand. Functionalism is more complex, because it maps from physics to computations to moral value. Moreover, while physics is real and objective, computations are fictional and "observer-relative" (to use John Searle's terminology). There's no objective meaning to "the computation that this physical system is implementing" (unless you're referring to the specific equations of physics that the system is playing out).
There's an important literature on what it means to implement a computation and whether functionalism is trivial. Some good starting points are
- Another article subsection I wrote on this topic: "What is a computation?". It explores many of the same ideas I'll discuss below, in slightly different words and more concisely.
- "Mechanical Bodies; Mythical Minds" by Mark Bishop.
- "Searle's Wall" by James Blackmon.
- "On Implementing a Computation", p. 315 of The Conscious Mind: In Search of a Fundamental Theory by David Chalmers.
- Gary Drescher's discussion of "joke interpretations" of physical systems in Good and Real.
I'll sketch one illustration of the idea below, inspired by Searle's famous "Wordstar" example, but my discussion here doesn't substitute for consulting other papers.
Example: Particles "implementing" a Turing machine
Consider a Turing machine that uses only three non-blank tape squares. We can represent its operation with five numbers: the values of each of the three non-blank tape squares, the machine's internal state, and an index for the position of the head.a Any physical process from which we can map onto the appropriate Turing-machine states will implement the Turing machine, according to a weak notion of what "implement" means.
In particular, suppose we consider 5 gas molecules that move around over time. We consider three time slices, corresponding to three configurations of the Turing machine. At each time slice, we define the meaning of each molecule being at its specific location. For instance, if molecule #3 is at position (2.402347, 4.12384, 0.283001) in space, this "means" that the third square of the Turing machine says "0". And likewise for all other molecule positions at each time. The following picture illustrates, with yellow lines defining the mapping from a particular physical state to its "meaning" in terms of a Turing-machine variable.
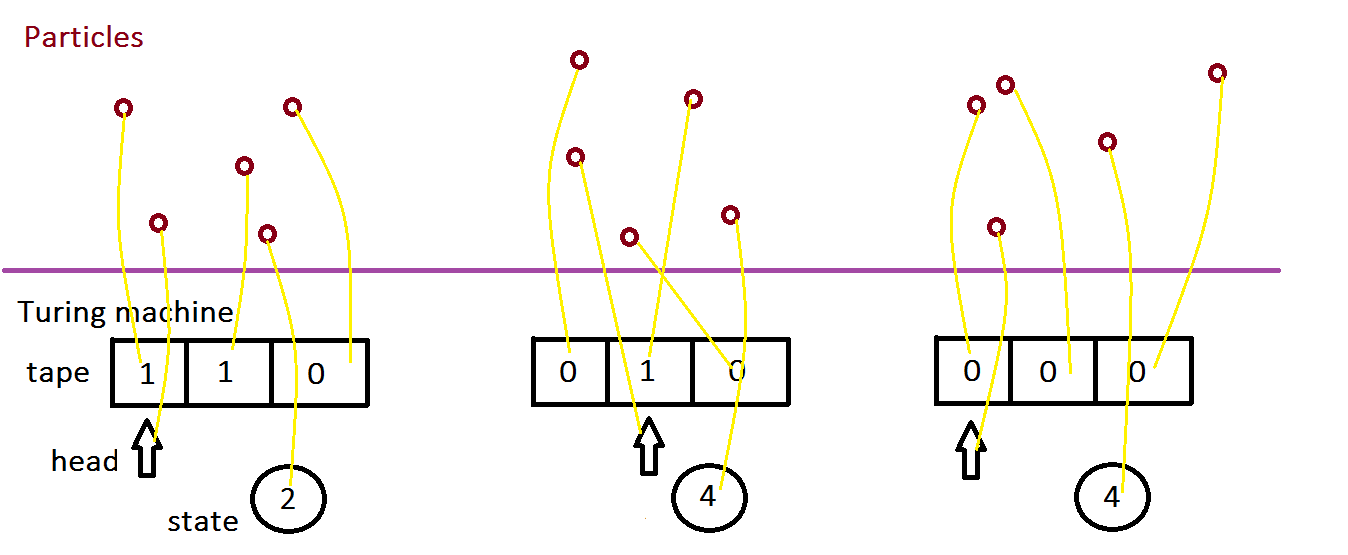
Paul Almond suggests that we may not even need five particles but that perhaps we could just attribute the "meaning" of a single electron as being the whole of a complex algorithm: "A small piece of wall can also be said to be implementing any algorithm [...] we like, if we are prepared to use a sufficiently complex interpretation. To take this to an extreme, we could even apply any interpretation we wanted to a single electron in an atom in the wall to obtain any algorithm we wanted." I'm not sure I buy this, because usually an implementation of a computation is defined as a mapping in which every computational state is represented by its own physical state. Of course, one could relax the definition of "implementation" to encompass Almond's proposal.
Representational arbitrariness in computer science
The arbitrariness of interpretation is a standard idea in computer science, as demonstrated by issues like signed number representations, character encodings, endianness, etc.
In addition, esoteric programming languages show that programs can be written using non-standard symbols, including color patterns and sounds. The arbitrariness of interpretation is easier to intuit when seeing this Ook! program rather than the equivalent in Java or Python. Of course, once the Ook! program is executed, the arbitrariness of interpreting the program syntax goes away, but it's replaced by arbitrariness of interpreting the computer's physical operations.
Interpretational indeterminacy also shows up in countless other domains, such as Rorschach tests, optical illusions, and literary criticism.
Using many possible interpretations?
As Blackmon observes, a computation (a logical object) is instantiated by both a physical system and an interpretation of the system. This leaves the question for functionalists: Which interpretation should be used when assessing the computation that a system is performing?
Almond suggests assigning a measure for how much a given system seems to implement a given algorithm. Inspired by this general approach, I propose that we could assign emotions and moral importance according to all possible interpretations at once, weighted by their plausibilities. In particular, let c(p,i) be a function that interprets physical system p as a computation c according to interpretation i. For example, with the five gas molecules pictured above, p is the set of gas molecules, i is the yellow lines, and c(p,i) is the Turing-machine states. Let S be the set of all interpretations. Let V(c) represent the moral value of computation c. And let w(p,i,c) represent the weight that we want to give interpretation i relative to system p, normalized so that for a fixed p, ΣS w(p,i,c) = 1. Then
overall moral value of p = ΣS V(c(p,i)) w(p,i,c(p,i)).
We could also construct functions Ex(c) that represent the degree to which computation c embodies emotion x. We could score each emotion using a similar formula as the above and then output the highest-scoring emotions as the text labels for what emotions the system is experiencing.
Peter Godfrey-Smith also proposes this idea of weighting different interpretations (p. 27): "I opt for a gradient distinction between more and less natural realizations (within systems that have the right input-output profiles)."
The next subsections discuss some factors that may affect how we construct the w(p,i,c) function.
Simplicity
More contorted or data-heavy mapping schemes should have lower weight. For instance, I assume that personal computers typically map from voltage levels to 0s and 1s uniformly in every location. A mapping that gerrymanders the 0 or 1 interpretation of each voltage level individually sneaks the complexity of the algorithm into the interpretation and should be penalized accordingly.
What measure of complexity should we use? There are many possibilities, including raw intuition. Kolmogorov complexity is another common and flexible option. Maybe the complexity of the mapping from physical states to algorithms should be the length of the shortest program in some description language that, when given a complete serialized bitstring description of the physical system, outputs a corresponding serialized description of the algorithmic system, for each time step. If interpretation i of physical system p has Kolmogorov complexity K, we might set w(p,i,c) ∝ 2-K.b
Note that such a definition would give much higher weights to computations that run for only a few steps, since then even gerrymandered interpretations wouldn't require huge complexity. It also vastly favors interpretations of physical systems as implementing extremely simple computations, since it's easiest if we just map the physical system to a small number of algorithmic states. For example, consider a finite-state automaton (FSA) that merely moves from one state to one other state on any input. For any physical process, we can just demarcate events before some time as the first state and events after some time as the second state, and we will have fully—and robustly!—implemented this algorithm. (This example draws inspiration from Hilary Putnam's famous theorem that "Every ordinary open system is a realization of every abstract finite automaton".)
Maybe our valuation V(c) of a short, simple computation c is so small that even though w(p,i,c) has high weight, this computation and others like it don't dominate overall utilitarian calculations. But it's also possible to bite the bullet and conclude that simple computations do dominate in ethical importance—bolstering other arguments as to why suffering in fundamental physics may overwhelm utilitarian calculations. After all, simple computations occur everywhere in physics, while complex computations like humans are exceedingly rare.
Reliability
Chalmers objects to gerrymandered interpretations like Putnam's on the grounds that physical state transitions aren't necessarily reliable:
consider the transition from state a to state b that the system actually exhibits. For the system to be a true implementation, this transition must be reliable. But [...] if environmental circumstances had been slightly different, the system's behavior would have been quite different. Putnam's construction establishes nothing about the system's behavior under such circumstances. The construction is entirely specific to the environmental conditions as they were during the time-period in question. It follows that his construction does not satisfy the relevant strong conditionals. Although on this particular run the system happened to transit from state a to state b, if conditions had been slightly different it might have transited from state a to state c, or done something different again.
Counterfactual robustness
A physical system implements one pass through a computation. But Chalmers and others believe a computation should be counterfactually robust, in the sense that the physical system should have correctly implemented a different branch of the algorithm had the inputs been different.
For instance, consider the algorithmc:
if the wind is blowing in London: Santa Claus visits New York otherwise: the Earth orbits the sun
Suppose there is no wind in London, and the Earth does orbit the sun. The physical system implemented one branch of the algorithm, but presumably it wouldn't have implemented the other branch had the input conditions been different. So interpreting the absence of wind as an implementation of this algorithm gets low weight—lower weight than the same algorithm would get if the world were such that Santa would visit New York if the wind blew in London, even if the wind still doesn't actually blow. Same physical event, same interpretation, but different weight depending on counterfactuals.
The most extreme case is to require counterfactual robustness and set w(p,i,c) = 0 unless all counterfactual branches of the computation c(p,i) would be implemented by p using the same interpretation i.
I share Mark Bishop's concern about the idea that counterfactual robustness is mandatory:
[Chalmers's view] implies the mere removal of a section of the FSA state structure that, given the known input, is not and never could be entered, somehow influences the phenomenal states experienced by the robot. And conversely the mere addition of a segment of [nonsense] FSA structure that, given the known input, is not and never could be entered, would equally affect the robot’s phenomenal experience...
Here's a more concrete example that doesn't rely on tenuous interpretations of physical systems. Suppose I have a complex Python program R that instantiates consciousness according to Chalmers. I run it on a specific input X. R uses many variables (e.g., to store values received from sensory input), but for the specific input X, they get set to definite values during execution, so we could just hard-code those values into the program from the outset. Doing this creates a new program R'. Now that variables have been fixed, we have less need for conditional branching, so we can remove branches of R' that aren't run, giving a new program R''. Chalmers's view suggests that R run on the input X is conscious, but R'', which implements only the operations that actually happen for input X, is less conscious even on the exact same input and even though it performs roughly the same logical computations, minus some overhead of branching and such.d
At times like these I'm glad to be an eliminativist about qualia, because if I were a Type-B physicalist, I would face some big headaches here.
Naturalness of representations
Maybe interpreting a physical object based on its "natural" properties is particularly elegant. Perhaps it's especially good if we represent numbers by the actual mass, or speed, or count of physical particles (relative to some units). So for instance, one could argue that representations of magnitudes in the brain by firing rates, neurotransmitter densities, and the like are more natural than representations of such magnitudes by binary numbers in computers, which can have many meanings depending on the type of representation scheme used (thanks to Tim Cooijmans for this point). That said:
- The greater complexity of mappings involving binary numbers should already be counted by the "complexity" aspect of w(p,i,c). For example, suppose we're looking for physical implementations of the computation c that represents addition of positive integers. Putting one atom next to another implements 1 + 1 = 2 in a fairly straightforward way. In contrast, a machine that implements the operation
0001, 0001 -> 0010
could mean 1 + 1 = 2 (addition) but could also mean other possible functions, like 8, 8 -> 4 if the binary digits are read from right to left, or 14, 14 -> 13 if "0" means what we ordinarily call "1" and vice versa, and so on. So interpreting this sequence of symbols as 1+1=2 seems more complicated. - For programs that aren't trivially short, we should be able to reduce the number of possibilities regarding which binary representation is being used based on how the program operates. See the next section for details.
- "Natural" numbers like neuron count and firing rate can still be semantically vague within the broader context of the algorithm. For example, some hypothesize that in the human brain, phasic dopamine represents positive reward-prediction error, while phasic serotonin represents negative errors, but it could just have easily worked the other way. More generally, a number within a complex computational system can mean many different things. For instance, suppose the numbers used to run a computer's scheduling algorithm were not binary but "natural", e.g., counts of little balls. Even if we could decode the numbers being shuffled as part of the algorithm, those numbers could have many possible meanings—e.g., ranks of items in a priority list, indexes of position in some other data structure, unique ids of an object, seconds elapsed since items were used, etc.
Other criteria
We're free to add other conditions to w(p,i,c) as well. Godfrey-Smith offers some suggestions (p. 29), though I didn't completely understand them. He notes that some criteria may introduce back traces of the "chauvinist" physical features on which functionalism was originally intended to remain neutral.
Constraint satisfaction for interpretations
We can focus on interpretations that are simple and counterfactually robust, since others get much lower weight in valuation calculations. Simplicity implies that the meaning of a given entity doesn't change willy nilly as the computation proceeds, because if meanings changed, the interpretation would need to specify where and to what the meanings changed. This means that, e.g., computation should generally use the same digital number and character representations throughout.
Based on these constraints, we may be able to make some further inferences about what interpretation fits the situation best. For example, suppose we have a physical system that looks like a reinforcement-learning agent, based on its counterfactually robust structure. Suppose that when the agent takes a given action A three times in a row, it receives rewards represented by the binary numbers 0011, 0110, and 0111. Following this, the agent continues to take the same action A. But now, when it takes action A three more times, the agent receives rewards 1111, 1011, and 1000. After this, the agent avoids taking action A again. One plausible inference from these observations is that the rewards are encoded based on a signed number representation (such as two's complement) in which positive binary numbers begin with a 0 and negative binary numbers begin with a 1. An unsigned number representation in which all the binary rewards received were positive is still possible, but it would require a more complex interpretation of the situation.
I'm not an expert on semantics, but I think the idea is similar to "Teleological Theories of Mental Content": "a theory of content tries to say why a mental representation [such as the binary number 1011] counts as representing what it represents. According to teleological theories of content, what a representation represents depends on the functions of the systems that produce or use the representation."
The process of identifying the most plausible interpretation is similar to scientific inference. Scientific theories are always underdetermined, with infinitely many possible theories to explain the same data. We overcome this problem by Occam's razor, penalizing more complex hypotheses. So one way to think about our weights w(p,i,c) is that they're probabilities in some sense.
Using Bayes' theorem?
One specific idea could be to pretend that the evolution of the physical system (plus all counterfactual evolutions, if we're insisting on counterfactual robustness) was/were generated by some random computation c according to some interpretation i. Since c is generally a high-level algorithm that doesn't specify all the detailed noise in the underlying physical system p, c can't generate p exactly. For instance, suppose that any voltage value less than 0.5 in some units represents a "0" bit, otherwise a "1" bit. Then any voltage has a symbolic meaning, but from seeing a "0" we can't infer the exact voltage value. To overcome this, we could imagine that, given a computational state and knowledge of the interpretation, there's a probability distribution for what the original physical state might have been. We could do this for every computational state and thereby generate a cumulative probability that computation c under interpretation i "produced" physical system p: P(p|c,i).
When inferring computations from physical processes, we want to go backwards: What computation and interpretation is plausible given the physical system: P(c,i|p)? These could be our weights w(p,i,c). By Bayes' theorem:
P(c,i|p) ∝ P(p|c,i) P(c,i).
The prior probability P(c,i) should embody Occam's razor by penalizing complex computations and interpretations. It might take the form 2-K for some appropriate Kolmogorov complexity.
P(p|c,i) is biggest for extremely elaborate computations, since the better the algorithm describes the full physical system, the more likely it is to predict the exact correct physical system in question. The extreme end of this is for the computation c to literally be the laws of physics of the system, with the interpretation i just mapping all entities onto themselves. In such a case, P(p|c,i) = 1, and c = p.
In contrast, P(c,i) is biggest for extremely simple computations. So maybe the product P(p|c,i) P(c,i) achieves some middle ground between extreme simplicity and extreme complexity?
Actually, P(p|c,i) P(c,i) is the same target metric that scientists use to evaluate physical theories: How well does the theory predict data, and how simple is the theory? So if the physical system runs for long enough ("accumulating enough data"), then maybe our metric w(p,i,c) = P(c,i|p) would just converge to the true laws of physics of the system. This is certainly a reasonable interpretation of what computation the system is executing, but it returns us back to square one. The functionalist goal was to interpret a system as implementing simpler, higher-level, more agent-like computations than the full messy details of what every quark and lepton is doing.
Higher-level computations
The problem of interpretational underdetermination for functionalism is usually discussed in the context of formal models of computation (finite-state automata, Turing machines, etc.), but unless we're using exact-match functionalism with the algorithms in the training set having very low-level specifications, it may be more enlightening to go a level up David Marr's hierarchy and focus on the general tasks that a cognitive system is performing, like stimulus detection, hedonic assessment, reinforcement learning, motivational changes, and social interaction. We have better intuitions about how much these processes matter than we do about, say, the moral status of particular transitions of a combinatorial-state automaton.
Assessing the degree of match between a physical system and these higher-level concepts is at least as fuzzy as interpreting a system as a specific formal computation, and we'll probably use vague concept matching to decide the weights for how much a given physical system implements a given high-level process. In theory, we could map from the physical system to a formal computation and then from the formal computation to a higher-level computation (ascending all three of Marr's levels), though in practice this is often more difficult than just noticing higher-level computations directly. For example, suppose we see a rabbit running away from a predator. It's easier to infer this as "escape behavior" directly than to map from the physical system to a formal specification of the computations in the rabbit's brain that produce its plans and movements and then to infer that those computations represent escape behavior.
We can have both sensible and joke interpretations of high-level computations. For example, suppose we define the high-level process of "reinforcement" as follows: "If the system does X, it continues to do X and does so to an accentuated degree".
- A non-joke system meeting this specification could be a falling ball, with X meaning "falling down" and "accentuated degree" meaning "falling faster". As the ball accelerates toward the ground, its falling behavior is reinforced.
- A joke system could be a ball that falls and hits the ground at time t = 5 seconds. Here, we define X as "falling before t = 5 s, or lying on the ground after t = 5 s" and "accentuated degree" as "having spent more seconds on the ground". The disjunction in the definition of X introduces complexity and gerrymanders away the natural interpretation of the situation, which was not reinforcement but rather cessation of the ball's original activity.
Interpretational relativity is not unique to functionalism
As Blackmon's paper makes clear, the idea that a high-level concept is relative to an interpretation is not a unique affliction of functionalism. Indeed, many descriptions above the level of base physics are open to joke interpretations.
For instance, let's take the beloved C-fibers of the type physicalists. What counts as a C-fiber? Something that has the structure of neuron clusters. If a specific molecular composition is not required, then we could interpret any chunk of matter as containing the structure of C-fibers, by mentally "carving out" the appropriate structure from the material, as a sculptor carves out a statue.e To represent the fibers as firing, we could imaginatively carve out successive snapshots of the fibers, animating their motion.
But maybe this approach is too liberal. Perhaps the type physicalists require that C-fibers contain carbon, hydrogen, oxygen, and other elements of Earth-like biology (a philosophy-of-mind version of "carbon chauvinism"). But then, we could presumably carve out C-fibers within at least many kinds of biological tissue. The molecules of, e.g., skeletal muscle wouldn't be in the same places as in neurons, but there's some gerrymandered mapping that puts the atoms of the muscle into the right places in logic-space to create something that looks more like an ordinary neuron.
Maybe type physicalists will exclude gerrymandered position swapping too. They could insist that the right elements must make up the right structures in their original spatial locations. At this point maybe joke interpretations fail, because the definition is so close to underlying physics. But of course, the definition is also quite chauvinist. There's a general tradeoff between definitions that are so narrow as to fail to capture everything important and so liberal as to capture many things that are unimportant. This is true not just for the spectrum from token physicalism (most chauvinist) to type physicalism (somewhat chauvinist) to functionalism with fixed inputs/outputs (less chauvinist) to liberal functionalism (anything goes!). It's also true for dictionary definitions, deontological principles, legal codes, and all manner of other instances where higher-level concepts are at play.
Revisiting the anti-functionalist argument
The observation that many high-level concepts are realized everywhere under some interpretation gives us new perspective on the anti-functionalist argument (advanced by Putnam, Searle, Bishop, and others) that consciousness can't be only algorithmic because a given algorithm is realized in any sufficiently big system under some interpretation. As an analogy, suppose I claimed that tables can't be structural entities, because the table shape is realized by any sufficiently big chunk of matter, under some interpretive "carving out" process.
If we understand why this anti-table argument is fallacious, we can see why the anti-functionalist argument is fallacious. Tables are what we take them to be. Some entities are more naturally construed as tables than others, and these are the ones we call tables. Likewise, algorithms are what we take them to be, and those processes that are more naturally construed as a given algorithm are the ones we say implement the algorithm. The reason some philosophers feel an intuitive difference between the table case and the consciousness case is that they insist that consciousness implies some extra property on top of physics, with there being a binary fact of the matter whether that extra property exists. But there is no such extra property. The reduction of tables is just like the reduction of consciousness—except that consciousness is wickedly more detailed and complex.
Functionalism as a sliding scale among physicalist theories
In "Absent Qualia, Fading Qualia, Dancing Qualia", Chalmers notes that functional description of a system depends on the level of detail at which it's viewed:
A physical system has functional organization at many different levels, depending on how finely we individuate its parts and on how finely we divide the states of those parts. At a coarse level, for instance, it is likely that the two hemispheres of the brain can be seen as realizing a simple two-component organization, if we choose appropriate interdependent states of the hemispheres. It is generally more useful to view cognitive systems at a finer level, however. For our purposes I will always focus on a level of organization fine enough to determine the behavioral capacities and dispositions of a cognitive system. [...] In the brain, it is likely that the neural level suffices, although a coarser level might also work.
But what are "the behavioral capacities and dispositions" of an organism? Are we only to count muscle movements? How about the behaviors that a locked-in patient can effect via pure thoughts when hooked up to a suitable recording device? What about the tiny but nonzero effects that your brain has on electromagnetic fields in its vicinity? What about the electron antineutrinos that are emitted from your brain during β- decay of carbon-14 in your neurons? Surely those are "outputs" of your cognitive system as well?
If the level of functional detail of the brain is taken to have fine enough grain, it can include the interaction patterns of specific molecules, atoms, quarks, or superstrings. Reproducing this level of detail would imply the kinds of requirements on physical substrate that type and token physicalists had been insisting upon all along—ignoring joke interpretations of superstring dynamics as seen in other physical systems. For instance, to reproduce the exact molecular functional dynamics of carbon-based biological neurons, you need biological neurons (ignoring joke interpretations of other physical systems as implementing biomolecule dynamics); artificial silicon replacements won't do. So there's a sense in which type/token physicalisms are just functionalism with a very fine level of resolution. Polger (n.d.): "one might suppose that 'functional' identity could be arbitrarily fine-grained so as to include complete physical identity."
On the flip side, behaviorism that omits consideration of internal states can be seen as functionalism with a very coarse level of detail—one that only cares about inputs and outputs (relative to some arbitrary definition of what counts as an input/output and what counts as an internal variable). A giant lookup table that implements a human can be equivalent in a behaviorist sense to a regular human because the level of functional detail that the theory demands is so sparse, at least on the inside of the person's skin.
So functionalism is not a single theory of mind but a continuum of theories that basically encompasses other physicalist theories. This isn't surprising, because there's not a single level at which abstractions operate. Abstractions can always be coarse-grained or fine-grained.
This point also suggests that when people claim "a digital upload of my brain wouldn't be fully me", they are right in a sense: The upload wouldn't implement all of the fine-grained functional processes that your physical brain does (e.g., atomic physics). Which processes count how much in the definition of "you" is a choice you can make for yourself. There's no metaphysical fact of the matter one way or the other.
How much do we care about various traits?
Sentience classification involves two stages:
- Identifying the traits of the physical system in question
- Mapping from those traits to high-level emotions and valences.
For exact-match approaches, step 1 amounts to picking out which training example(s) (if any) the physical system implements, and step 2 amounts to just reading off the answer(s) found on the training label(s).
Step 2 is less trivial for fuzzy-match approaches. In these cases, we have to decide, e.g., how bad it feels to have C-fiber firings (type physicalism) or to broadcast a negative reward signal (functionalism). Following are some ways we might decide this.
Learn from training examples
If we place a lot of faith in our intuitive judgments, we could apply standard machine learning to train a neural network or other function approximator to map from concepts like "reward-signal broadcast intensity" or "C-fiber firing intensity" to emotions like "happy" or "pain" and valences like +5 or -20.
Neural networks in our own brains produce these kinds of outputs in the form of verbal reports, and presumably artificial classifiers hooked up to brain signals could become reasonably accurate at predicting human-reported brain states. Extending neural-net hedonic predictors to animals and animal-like digital creatures would be trickier due to lack of verbal reports, though behavioral measures might serve as proxies for welfare in order to train the nets.
Where this kind of hedonimetry becomes trickiest is for very simple or very alien minds. But maybe we should just take it on faith that the weights learned from familiar examples would transfer appropriately to unfamiliar cases. We could also sanity-check and hand-tweak the weights and outputs for the atypical kinds of minds.
Anthropomorphize
How much do we care about a cartoon in which a character gets beat up? Maybe it's proper not to care at all. But if we did want to extend the slightest of sympathies, how would we do this? The method just discussed would tease out some very crude functional behavior implied by the moving TV-screen pixels and then feed that into a trained classifier. But another approach is to more directly feel out the situation via anthropomorphism.
Yes, I know: Anthropomorphism is a dirty word, and no one wants to be accused of it. But most of human ethics is anthropomorphic to some degree—we assess goodness/badness, in some measure, based on projections of our minds onto other things. The classifier-training approach just discussed is anthropomorphic insofar as atypical minds are evaluated based on pretending their classifier inputs came from humans (and maybe other intelligent animals).
We could also make judgments more directly about our abused cartoon character, without any explicit classifier, by projecting ourselves into the character's situation. In doing so, we should try to imagine ourselves as the simplest possible mind that we can conceive of being, though this fantasy will still be vastly too complex to actually resemble the mind being approximated. We can then try to rationally strip away extraneous cognitive processes that the simple mind clearly doesn't have. In the end, we'd be left with a tiny sliver of moral valence, so small as to be almost nonexistent. But at least this exercise might help us intuit whether we think beating up the cartoon character is (infinitesimally) good or whether it's (infinitesimally) bad (or, if we're negative utilitarians, whether beating up the character is neutral or bad).
In "Appearance vs. implementation", I discussed how visual display underdetermines anthropomorphic interpretations, in a similar way as physical processes underdetermine computational interpretations. For instance, does the abused cartoon character suffer from being beat up, or does he have a different physiological constitution in which physical injury is actually fun? In literal terms, this question is absurd: The character has no physiology as we know it and can't meaningfully be said to suffer or enjoy the experience. Musings about whether the character is pained or pleasured are basically fantasy, since moving pixel patterns on a screen are so vastly simpler than human feelings that almost everything we imagine about emotion doesn't apply. Still, if we're going to (dis)value the cartoon character at all, then fantasies of this type might give us some grounding for doing so. Of course, the number of cartoons in the world is so small that this particular question is morally trivial, but similar questions arise when valuing simple processes in fundamental physics, and in that case, numerousness can blow up even the tiniest grains of moral concern for any given system to astronomical proportions aggregated over all the systems.
Anthropomorphism probably unconsciously infects our judgments about the valence of various computational processes, because memories and concepts of high-level human experiences may be activated to some degree when thinking about simpler systems. Explicit anthropomorphic fantasizing is another route to a similar effect.
All of that said, I feel very reluctant to anthropomorphize deliberately, because doing so obviously commits the pathetic fallacy.
Assess mental processes directly
Rather than training from examples, we can try to theoretically judge how much we care about psychological/computational processes of aversion, anxiety, reward learning, memory formation, self-reflection, and so on. No doubt our feelings here will be swayed by actual examples that we have in mind. There's also a risk of developing abstract principles that are too focused on elegance and insufficiently tied to empathetic reactions.
Summary of our classifier
The following diagram illustrates how our overall sentience classifier might work on a given physical system. (The picture appears cut off on purpose, because I'm trying to illustrate that there can be lots of inputs to the classifier beyond those shown here.)
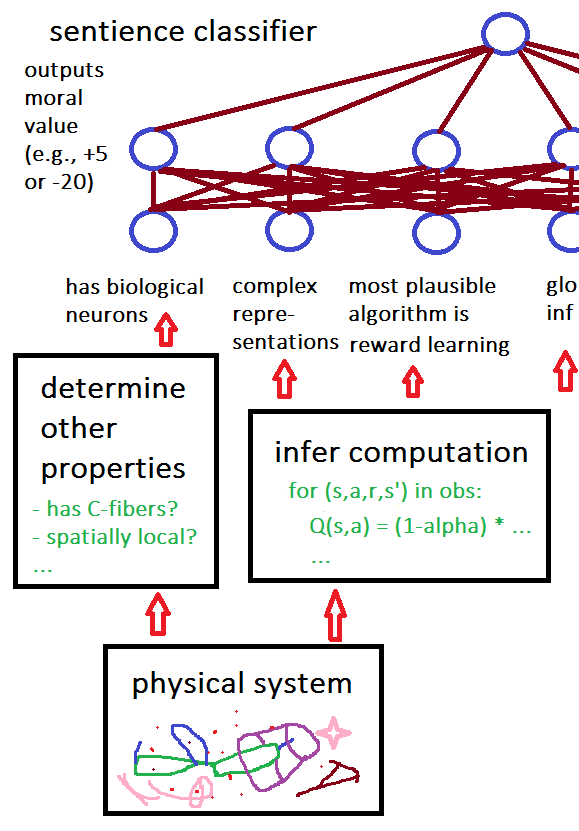
The neural network at the top of this diagram outputs moral value (the V(c) function for functionalists). It's a function of only one algorithmic interpretation of the system, but we could alternatively run this network for all possible underlying algorithms c and weigh the resulting network outputs based on the plausibilities of the interpretations that yield each different c. Also, the particular network in this diagram outputs the moral valence of the computation, but we could have other neural networks to score the physical system on various conceptual attributes, like "happy" or "fearful", and then choose top-scoring labels to verbally describe the system.
Something vaguely like this classifier architecture may already exist in our brains—presumably with lots of additional complexities, such as modification of the outputs based on cached thoughts, cultural norms, resolution of cognitive dissonance, etc. Also, the networks in human brains
- are probably much messier and more computationally complex
- have more levels
- include recurrent loops.
Optional: Personal history with this topic
When I began discussing utilitarianism in late 2005, a common critique from friends was: "But how can you measure utility?" Initially I replied that utility was a real quantity, and we just had to do the best we could to guess what values it took in various organisms. Over time, I think I grew to believe that while consciousness was metaphysically real, the process of condensing conscious experiences into a single utility number was an artificial attribution by the person making the judgment. In 2007, when a friend pressed me on how I determined the net utility of a mind, I said: "Ultimately I make stuff up that seems plausible to me." In late 2009, I finally understood that even consciousness wasn't ontologically fundamental, and I adopted a stance somewhat similar to, though less detailed than, that of the present essay.
In some sense, this piece is a reply to the "you can't measure utility" objection, because it outlines how you could in principle "measure" utility, as long as you started with (1) input training data consisting of judgment calls about how good/bad certain experiences are and/or (2) general principles about how much various cognitive processes matter. Of course, in practice, precise measurements are out of the question most or all of the time, but we can hope that cheaper approximations work well enough. That a quantity is hard or impossible to compute doesn't mean it's not the right quantity to value; better to approximate what you actually care about than to optimize for some other, more tractable quantity that you don't care about.
Appendix: Other implications of interpretational relativity of computations
Anthropic reasoning
It's common for computationalists to think in terms of algorithms: "I am the algorithms in my brain, no matter on what substrate they're implemented." This is not just a poetic statement of personal identity but also may translate into consequences for anthropic reasoning.
For instance, suppose a person's brain is uploaded to software. One copy is run in a blue room, and two copies are run in a red room, but no upload has light sensors to see its room's color. All copies run from the same starting conditions and with the same environmental inputs. Hence, all three "instances of the algorithm" should be identical (in logical space, though not physical space).
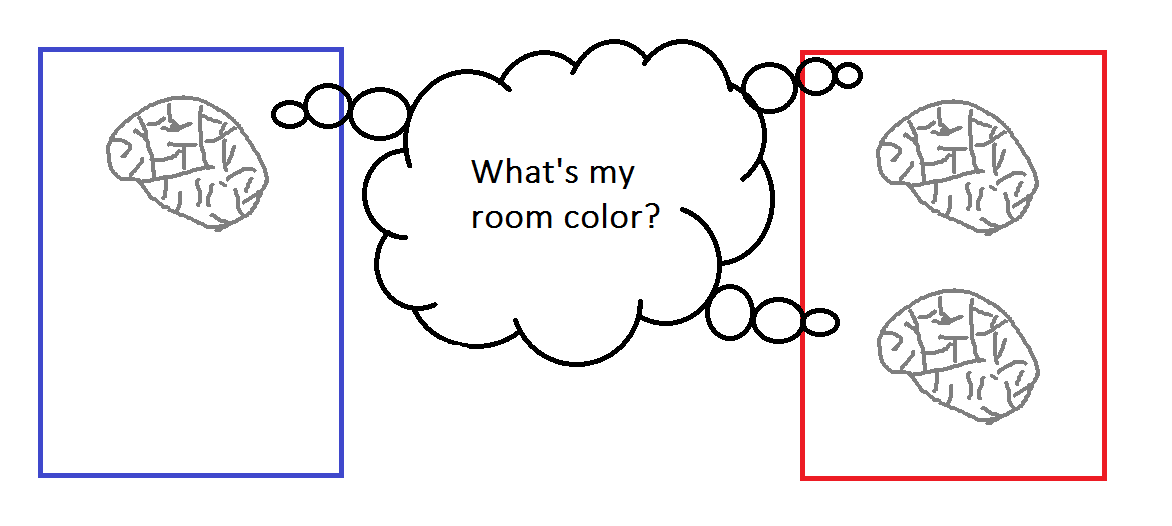
Naive anthropic reasoning might run thus: I could be any of the three copies, and since they're subjectively indistinguishable, I should assign equal probability to being each one. Therefore, if I have to bet money on whether my room is blue or red, I should bet on red, since I have a 2/3 chance of winning in that case.
This way of thinking implies a notion of "I" that's tied to a specific cluster of atoms. It's true that any given cluster of atoms computing you has a 2/3 chance of being in the red room. But most of the time we think of "I" in the sense of "these thoughts that are happening", and the same thoughts are happening for all three instances of the software jointly. It may be better to think of "I" as the collection of all three copies together (thanks to a friend for pointing this out), since what one copy does, the others do, at least until they diverge. (For instance, when the bet winnings are paid out, the copies in the red room diverge from the one in the blue room.)
But what happens when we recognize that "your algorithm" is not an ontological primitive? In a sense, your algorithm is running in any sufficiently big physical system under some interpretation. Fortunately, this is not a cause for ontological crisis, because physicalists always recognized that anthropic reasoning doesn't track any "right answers" fundamental to the universe but is merely a strategy that can be applied to help with decisions. Whenever you get confused, you can always return to safety by remembering that only physics is ontologically primitive, and everything else is fiction.
Should your software copies also identify themselves with gerrymandered interpretations that are running in the wall of a house, in the center of the sun, and so on? There's no right answer to this question, because what constitutes "you" is not ontologically fundamental. You can extend your identity as widely as you want. We don't have an anthropic puzzle about why you aren't the atoms in your wall because "you" are not a localized thing. There may indeed be traces of the thoughts you're having now in your wall, and that's fine. You can kinda sorta be your wall and the center of the sun and digital uploads all at once. Defining "you" is just poetry.
None of this interferes with your algorithm's ability to make choices about how it wants the world to change. If your algorithm chooses action A, this yields world X, while if it chooses action B, this yields world Y. Your algorithm can morally evaluate worlds X and Y, decide which it prefers, and let that inform its choice. The kinds of moral valuation discussed in this piece could play a role in evaluating X vs. Y, even if you're purely an egoist who nonetheless extends some sympathy to your gerrymandered interpretations in building walls.
A good practical reason to focus on non-gerrymandered interpretations is that physical systems which robustly implement the algorithm that you identify with are most likely to actually follow through on the choices you make. For instance, if your algorithm bets on being in the red room, all three software copies of the algorithm actually proceed to implement that bet, since software has robust implementation. Meanwhile, almost all the copies of your algorithm in the walls of buildings that had been identical up to that point cease to be identical on the next step, because the gerrymandered mappings that worked previously don't actually predict the next steps of the physical system. Of course, we could, post hoc, invent further mapping rules that would make the walls continue to track your algorithm, but assuming we give extraordinarily low weight to gerrymandered interpretations, we don't care much about that, so we can focus mainly on the effects of your algorithm's choice on the physical systems that robustly implement it.
In other words, if the algorithm wants to produce a physical state in which the physical systems that it most identifies with win as much money as possible, it should bet on being in a red room. That will imply that two of the three systems it identifies with win their bets. If instead the algorithm is fine identifying with joke interpretations of itself, pretending that the walls of buildings contain copies of it winning money regardless of what happens to the software copies in the colored rooms, then it doesn't much matter what it chooses.
This point is similar in spirit to the claim that you should act as if you're not a Boltzmann brain, because if you are a Boltzmann brain, your choices will have virtually no predictable impact, since the molecules that compose you will almost instantly reorganize into meaningless noise. In some sense, Boltzmann brains are actual physical manifestations of gerrymandered algorithm interpretations that already logically permeate the universe. While I haven't thought about the matter rigorously, I have some intuition that the interpretational weight that a gerrymandered mapping of my brain should get in an arbitrary physical substance like the wall of a building should be similar in magnitude to the probability of random particles forming a Boltzmann brain per unit time. This is because I imagine the mapping from physics to algorithm as if it were little ghostly arrows moving around randomly to specify the interpretation. Arrows move around and eventually point in the right ways to create an interpretation of a brain, just like Boltzmann brains form when particles move around and eventually combine in the right ways to create the structure of a brain.
Ontology of consciousness
It's common to hear claims like:
- "Consciousness is a self-reflection algorithm of some sort."
- "Our phenomenal experiences are functional processing."
There are different ways of understanding these ideas:
- Worse Way: Consciousness is algorithms that get instantiated by physics. Or: Consciousness reduces to algorithms.
- Better Way: Consciousness is physics, which can be approximately modeled by algorithms. Or: Consciousness reduces to algorithm-like physical processes.
Unfortunately, I'm often guilty of the Worse Way of thinking in other essays. The reason the Worse Way is problematic is that algorithms other than the laws of physics are not ontologically primitive. The Worse Way can encourage us to imagine that algorithms are somehow disembodied ghosts, which inhabit physical systems that implement them appropriately. But as we've seen with triviality arguments against functionalism, these ghosts would have to inhabit every sufficiently big physical system.
As usual, we can illustrate the same point in the language of tables:
- Worse Way: Tables are structures that get instantiated by physics. Or: Tables reduce to structures.
- Better Way: Tables are physics arranged in a kind of structural shape. Or: Tables reduce to table-structured physical substances.
Speaking of "structures" in the abstract might encourage a kind of Platonism about the ideal "form" of "tableness". That said, I think this kind of misguided Platonizing is more likely in the case of algorithms, since they're more mathematical.
The "is" in the statement "Consciousness is physics" doesn't mean identity between properties (which would be property dualism) but merely that "consciousness" is a poetic name that we give to certain types of physics, in a similar way as "table" is a poetic name we give to certain other types of physics. For that matter, "algorithms" are also poetic names for certain types of physics—labels that apply more strongly to "good" interpretations than to "joke" interpretations—and when we appreciate this, it's fine to say that "consciousness is algorithms". It's just very easy (for me, at least) to fall into the trap of reifying algorithms as crisply defined objects in their own right. We need to remember to let physics be physics. Any additional structures that we impose on it are in our heads.
The differences between good vs. joke interpretations of a system are easy to see from a third-person perspective. The intentional/cognitive stance of attributing certain mental algorithms is useful when applied to humans and animals. For example, suppose we have a functional model of a dog's brain, and we read off from that model that its thirst signals are firing. From this knowledge, we can predict that in the near future, the dog will go in search of its water bowl. However, such cognitive modeling is not useful when applied to walls. Suppose we try to claim that the dog's mental algorithms are actually instantiated in the wall under some interpretation of wall molecule movements. You say that under some interpretation, the wall right now is instantiating thirst signals in the wall_dog's brain; for example, you claim that some particular molecule movements represent the thirst signals, which are affecting other molecules that represent other parts of the brain. Given this information, can you predict subsequent facts about the physical evolution of the wall? For example, can you predict which molecules will move where? No, the "wall is a dog brain" interpretation doesn't help at all here. The wall's molecules will move in some apparently random way, and your dog-type cognitive model of them doesn't robustly track the actual causal dynamics of the physical system.
In this sense, mental algorithms are just models for predicting heterophenomenology, in a similar way as supply and demand curves are just models for predicting the prices of goods. We shouldn't apotheosize algorithms to a higher status than they deserve.
Acknowledgments
Comments by Carl Shulman kicked off some of my explorations that motivated this piece. A few of my proposals may have been partly inspired by early drafts of Caspar Oesterheld's "Formalizing Preference Utilitarianism in Physical World Models". Adrian Hutter corrected a mathematical error in one of my footnotes.
Footnotes
- Chalmers discusses encoding Turing-machine states in a similar though not identical way. Curtis Brown comments on this proposal, claiming that Chalmers's combinatorial-state automaton (essentially, a list of vectors) isn't a good model of computation because it's more complex and less transparent than a Turing machine and because it can implement any computation in one step or even perform non-computable tasks. (back)
- Almond calls such programs "algorithm detectors" and proposes a similar idea:
If an algorithm detector can produce some algorithm A by applying a short detection program to some physical system then we should expect many other detection programs also to produce A. If, however, we need a very long detection program to produce some algorithm A when it is applied to the physical system, we should expect interpretations that produce that algorithm to be rare.
Note that I only read the details of Almond's paper after writing the bulk of this one, so he and I seem to have converged on a common sort of idea. (back)
- Normally algorithms are conceived of in abstract, mathematical terms. Algorithms of that type may be more precise, but they're not more "real" in any ontological sense, since, as we've seen, all algorithms are fictional, except for the algorithms of base-level physics. (back)
- I'm also assuming that the computer doesn't use speculative execution, i.e., that it doesn't implement branches preemptively and then discard them if they were the wrong branches, since if it did, then some counterfactual branches that are absent from R'' would be partly implemented by R. (back)
- Almond discusses this idea in "Objection 10" of his piece: "What you say about algorithms, you could as easily say about physical objects. For example, the concepts of 'cat' or 'chair' could be expressed as interpretive algorithms that allow us to decide if these objects are there. The problem is that we might imagine making a very complex interpretation that allows us to find a cat or chair, when none is apparent in the real world. Is this supposed to mean that such objects exist in some sense?" (back)