Zooplankton Densities in Lakes and Reservoirs

By Brian Tomasik

First published: 11 Dec 2016. Last nontrivial update: 11 Dec 2016.

Summary

This page presents estimates of (metazoan) zooplankton densities in freshwater lakes and reservoirs. On average, zooplankton densities are around ~101 to ~102 individuals per liter, sometimes higher and sometimes lower.

Contents

Snow (1974)

Snow (1974) found an average of 139.7 zooplankton (rotifers + cladocerans + copepods) per liter of water in a Wisconsin lake.

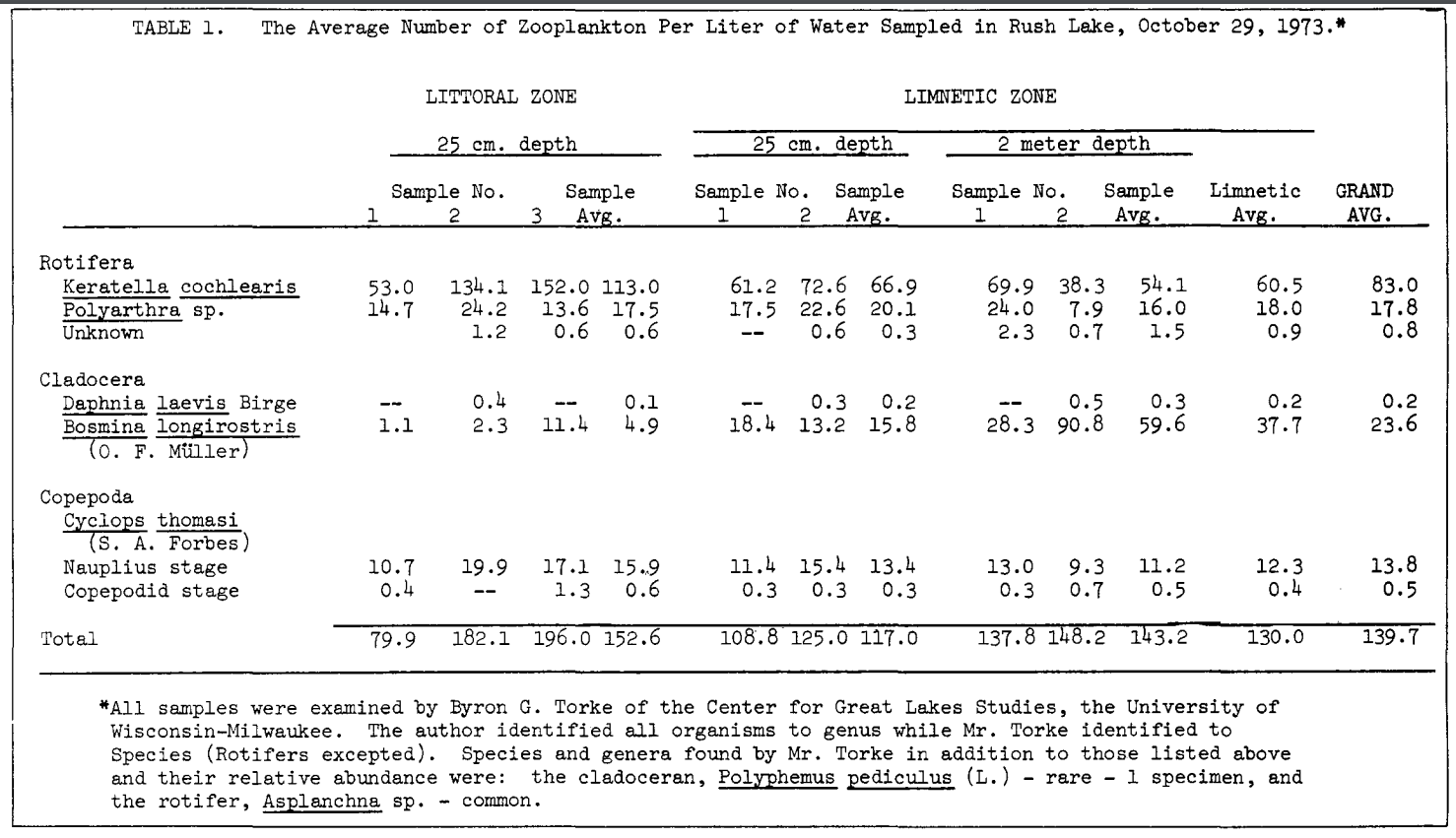
It should be noted that these zooplankton measurements were taken six years after the fish toxicant antimycin was used in the lake. However, the author believes (p. 3) that "the very presence of the organisms noted in 1973 is prima facie evidence that no gross long-term detrimental effects to these organisms occurred as a result of the use of antimycin."

Pinto-Coelho et al. (2005)

Pinto-Coelho et al. (2005) give the following table. I put a blue square around the most relevant numbers. (Maximum densities are interesting but by definition shouldn't be taken as typical.)

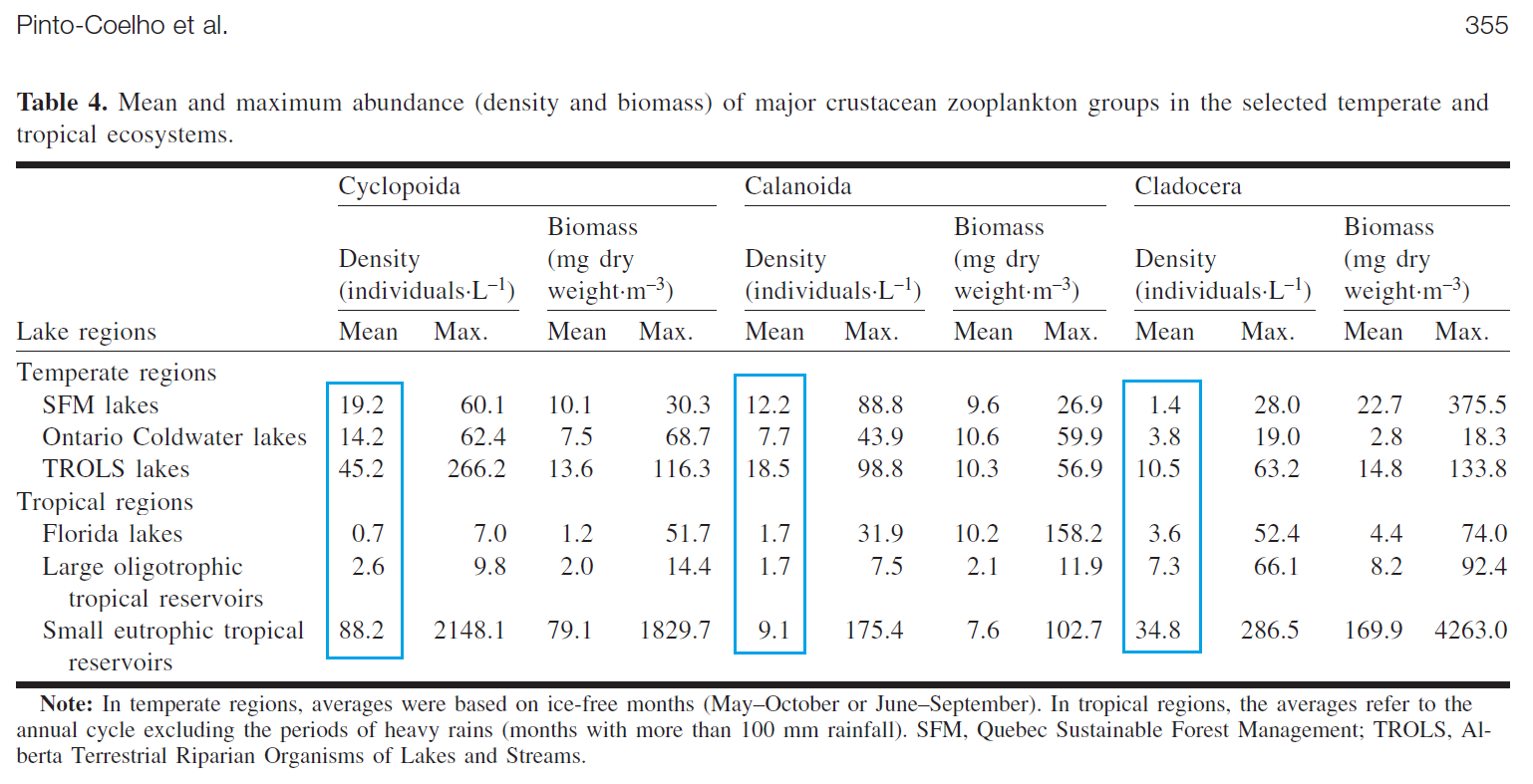
The authors explain regarding sampling: "In this study, most of the zooplankton were collected in the whole water column with vertical net tows of small mesh size nets (53–150 μm) that retain most adult crustaceans" (pp. 349-50).

Ahmed (2010)

Ahmed (2010) sampled "Reservoirs at the Clayton County Water Authority" in Georgia, USA, using a vertical tow (p. 14). A vertical tow samples "the plankton throughout the water column" rather than just at the surface.

Ahmed (2010) reported the following densities per unit area, which I assume means the entire depth of the water column for that amount of area.




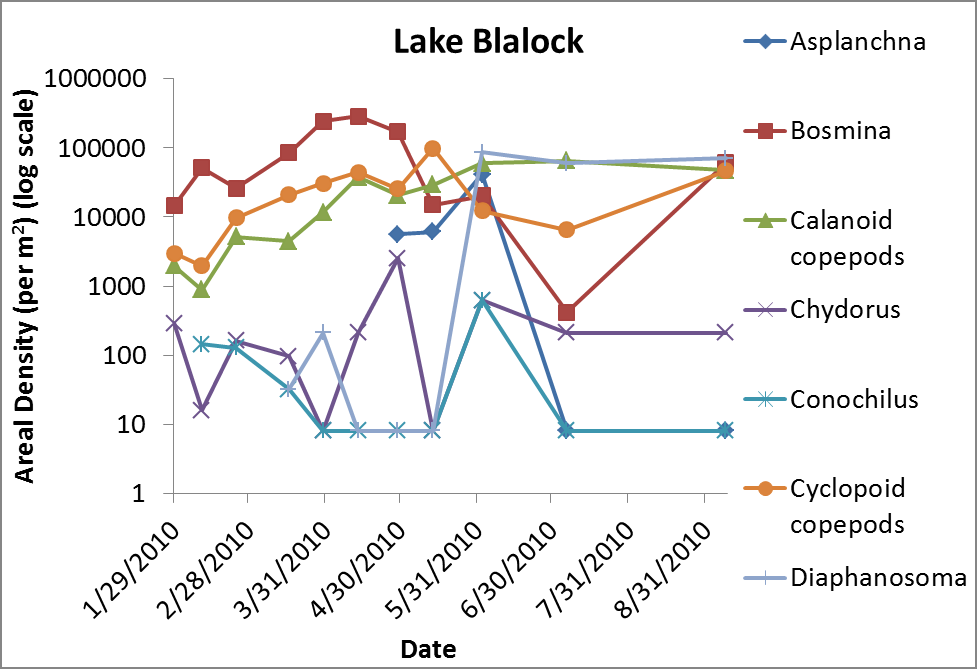
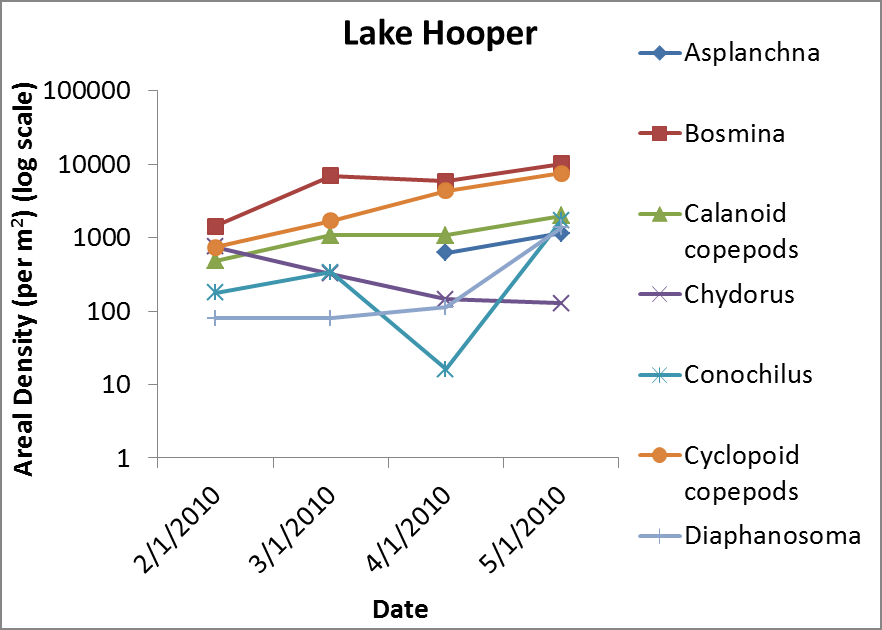
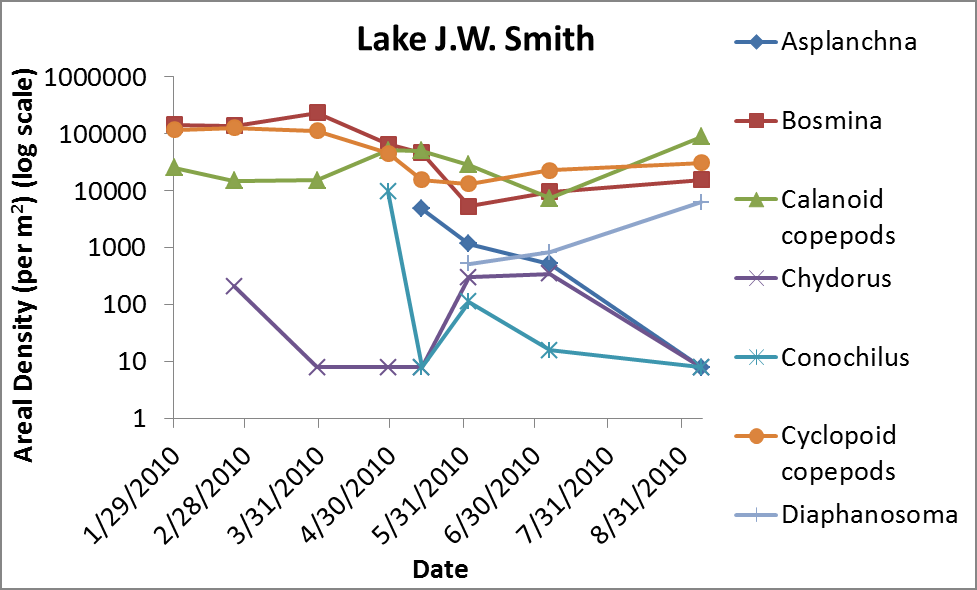
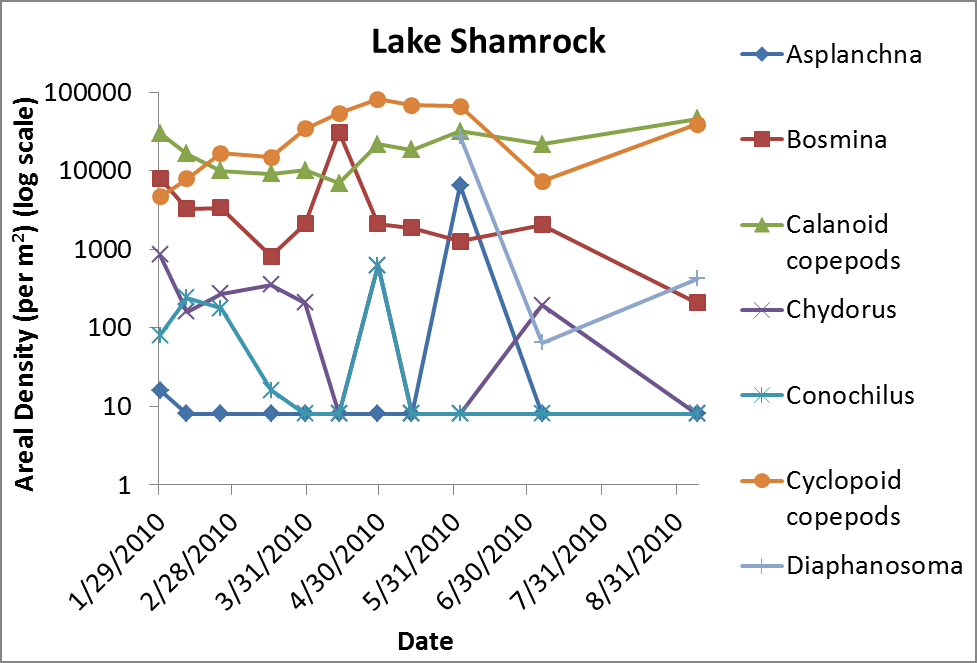
If the lake is D meters deep, 1 m2 of area would correspond to D m3 = D * 103 liters of volume. I don't think Ahmed (2010) specifies the depths of the lakes, but assuming D is on the order of ~101 ma, then 1 m2 would correspond to about 104 L. Hence, dividing the abundances in the graphs by 104 may give approximations of densities per L.

Footnotes

  1. I would guess that many regular reservoirs have depths on this order of magnitude. For example, this report on a reservoir near my home town measured a depth of 8.82 meters (p. 9, Table 1) at "Location 1", which "was chosen to be the deepest spot that could be found" in the reservoir (p. 7).  (back)