Summary
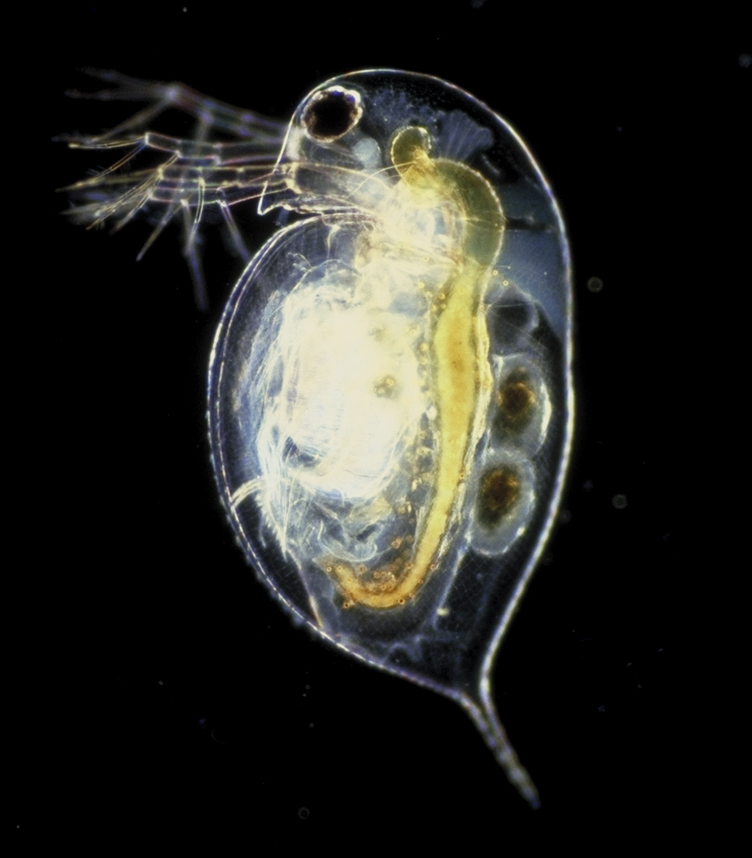
Many types of systems can be used for wastewater treatment, one of which is facultative lagoons. Kring et al. (2013) measured zooplankton in two "facultative aerated wastewater treatment lagoons" (p. 1973) in Canton, New York. Based on this study, I perform a very rough calculation which suggests that the wastewater generated by the average Canton resident gives rise to an extra population of ~200,000 Daphnia pulexa on an ongoing basis in the wastewater lagoon, not to mention additional copepods and other zooplankton as well. However, it's unclear whether this is more or fewer invertebrates than would exist if the lagoon land area were covered by grass instead of water.
Contents
Introduction
Kring et al. (2013) explain (p. 1974):
In the USA, aerated wastewater lagoons are frequently used to treat industrial and municipal wastewaters. [...] In aerated lagoons, bacteria, yeasts, and algae are the food source for zooplankton, particularly rotifers and crustacean cladocera. The role of the zooplankton includes the grazing of particles, other microflora, and phytoplankton that result in the clarification of the wastewater and lower BOD.
Kring et al. (2013) propose the idea of (painfully) killing zooplankton in wastewater-treatment lagoons for biofuel. The authors examined "two [...] facultative aerated wastewater treatment lagoons" and found (p. 1973):
In terms of biomass, the cladoceran Daphnia and the copepod Cyclops were the dominant zooplankton in these hypereutrophic lagoons, while unicellular chlorophytes dominated the phytoplankton community. Secondary productivity of these lagoons (250 g of dry weight m−2 yr−1) is comparable to the secondary productivity of other sewage lagoons.
Zooplankton biomass created per capita
The wastewater "facility serves 8600 residents of Canton, which includes two local colleges", although "The third lagoon was turned off and bypassed during the summer months due to seasonal decreases in effluent production caused by the departure of the college student population from the area" (p. 1974).
The authors found (p. 1977) that Daphnia pulex had an average biomass, across the two lagoons measured, of (1.77+1.13)/2 = 1.45 g dry weight per m2 and that copepods had an average biomass, across the two lagoons, of (1.65+0.88)/2 = 1.27 g DW per m2. The lagoons also contained other zooplankton not counted here, such as rotifers (p. 1977). That said, I personally wonder whether these biomass estimates are slightly too high, given that they're based on "Surface samples (z < 1 m) [that] were taken at three locations in the lagoon" (p. 1979), while the whole lagoon "has a maximum depth of 4.6 m" (p. 1974). If zooplankton were more numerous in the top meter of water (such as due to more light being present near the surface, feeding more phytoplankton there??), then these estimates would be somewhat inflated, since the authors assumed that zooplankton densities were constant throughout the depth of the water column (p. 1976, eqn. 1).
"Each lagoon is 183 m × 91 m" (p. 1974), so total zooplankton biomass of D. pulex + copepods would be (2 lagoons) * (1.45 + 1.27 g DW per m2) * 183 m * 91 m = 91,000 g DW. Then dividing by 8600 residents (which may be too high, since college students aren't there all year) gives 91,000 / 8600 = 11 g of zooplankton dry weight of standing biomass created by the average resident. Keep in mind that this biomass is not just supported by decomposition of human waste but also by phytoplankton living in and gathering nutrients from the ponds.
Number of D. pulex created per capita
How many individual animals does the above biomass represent? I'll just do a calculation for D. pulex to give a flavor, but one could do it for the copepods as well.
Kring et al. (2013) don't say the average weight of D. pulex, but they do say they used the following information from this source in order to calculate dry weights:
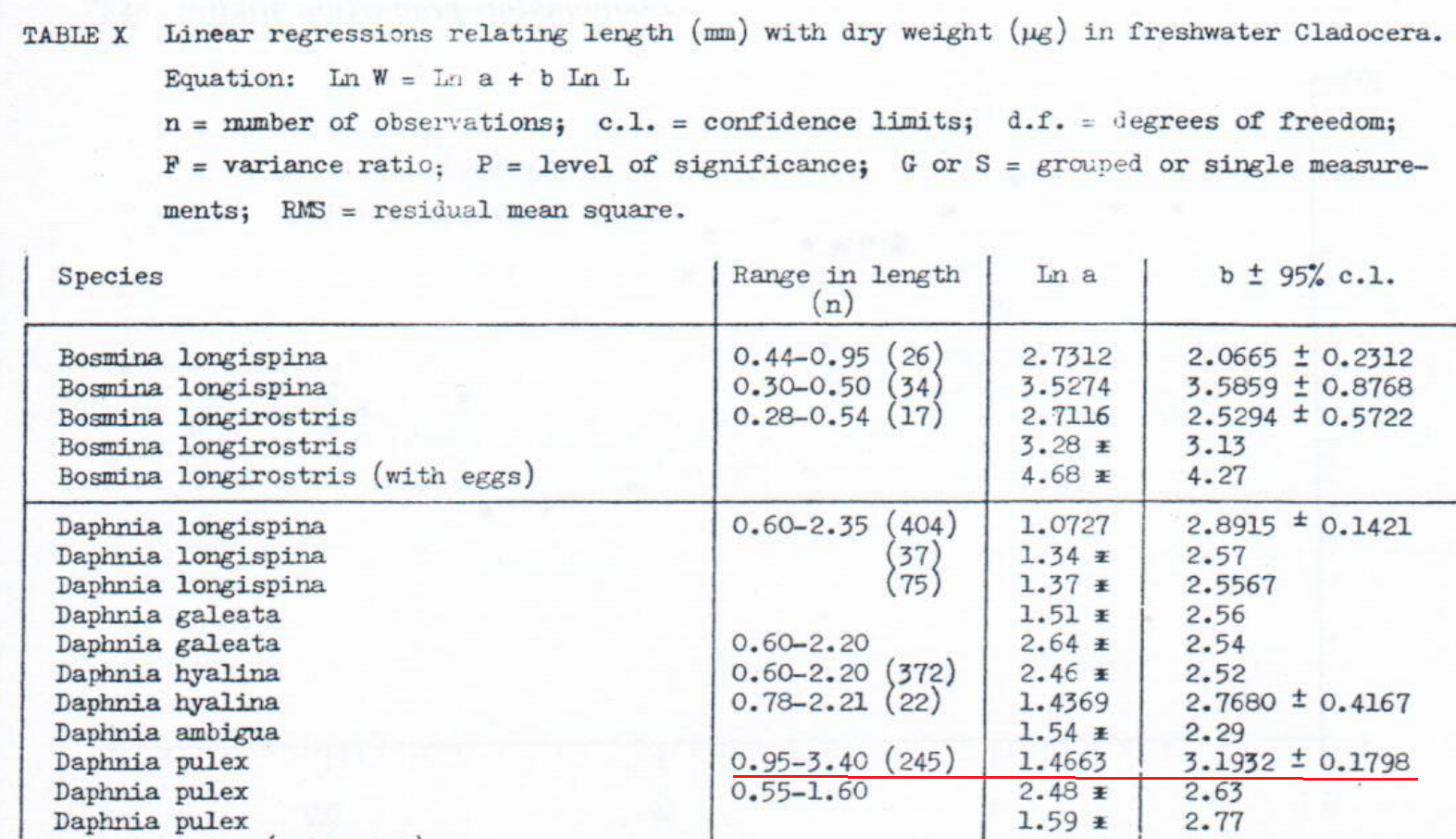
Kring et al. (2013) took L to be "the geometric mean length of individuals in the sample population" (p. 1976). I don't have Kring et al. (2013)'s length-measurement data. But the above picture reports a range from 0.95 mm to 3.40 mm. The geometric mean of those two endpoints of the length range is 1.8 mm, which I'll use. Then, ln W = 1.4663 + 3.1932 * ln(1.8) = 3.3, so that W = e3.3 = 28 μg.b
Each person produces a standing D. pulex biomass of roughly (2 lagoons) * (1.45 g DW per m2) * 183 m * 91 m / 8600 people = 5.6 g DW, which translates to 5.6 / (2.8 * 10-5) = 2 * 105 individual D. pulex!c
This is similar to the number of dust mites that an individual person gives rise to (105 to 107), although dust mites are a bit smaller (0.2-0.3 mm) than D. pulex.
Prevented terrestrial invertebrates
While facultative lagoons create significant suffering from aquatic invertebrates, they cover over land that would otherwise produce terrestrial vegetation, such as lawns, farmland, or woods.
Here's a picture of the Canton lagoon and its surrounding vegetation, based on the coordinates given in Kring et al. (2013), p. 1974.
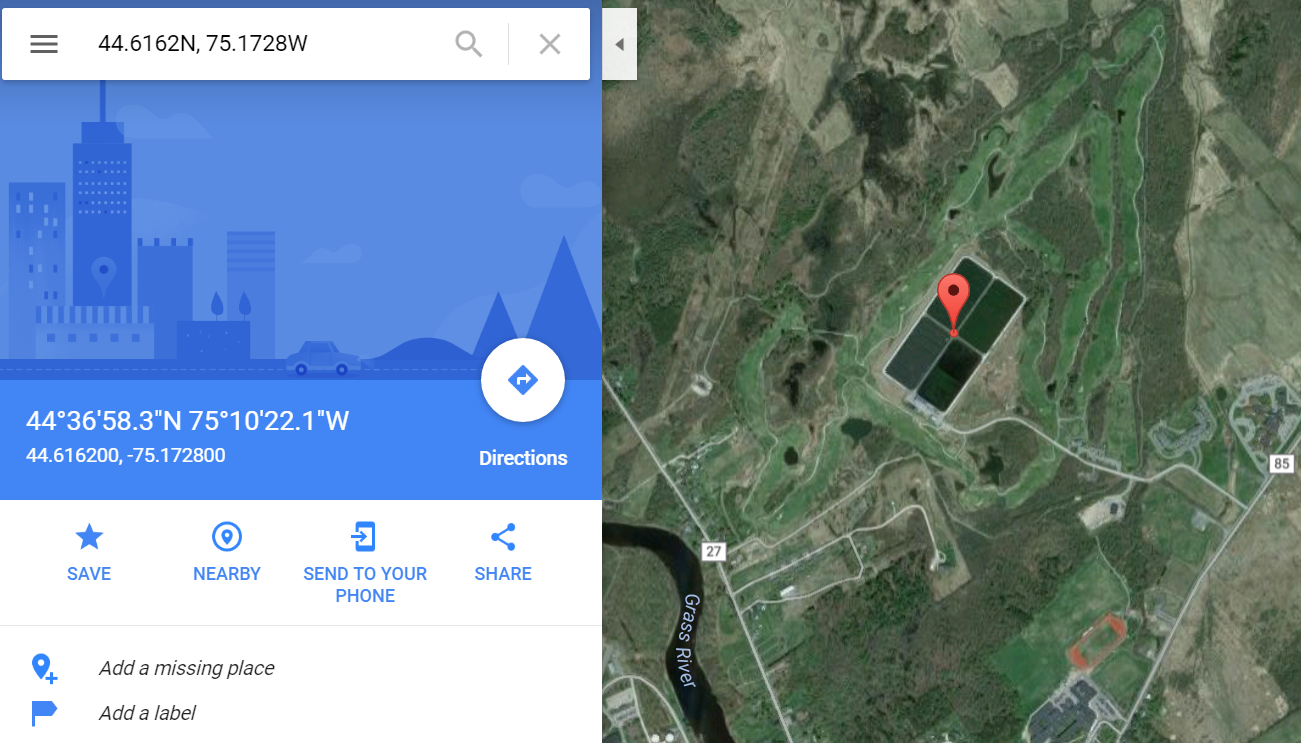
The Canton lagoons are each 1.7 hectares (p. 1973), plus some extra area around the edges.
Suppose that if this lagoon facility didn't exist, the land would instead be covered by grass. Grassy areas can support springtail populations of 104 to 105 per m2, not to mention mites and numerous other invertebrates.
Above I mentioned an average biomass of D. pulex of 1.45 g dry weight per m2 in the lagoons, which translates to roughly 1.45 / (2.8 * 10-5) = 52,000 D. pulex per m2. Like the springtail estimate, this falls in the range 104 to 105 individuals per m2.
Thus, without further information, it's unclear whether facultative lagoons create or prevent net invertebrate suffering. Their large area allows them to carry out significant photosynthesis, which is bad, but their large area also implies that they prevent lots of land plants from growing.
Footnotes
- Here are some videos of this animal to give a sense of its intelligence: one, two. (back)
- Using the lower length estimate of 0.95 mm, we would have W = 3.7 μg, and using the upper length estimate of 3.40 mm, we would have W = 220 μg. (back)
- Using the lower-bound mass estimate from the previous footnote, we would have 5.6 / (3.7 * 10-6) = 1.5 million individual D. pulex. Using the upper-bound mass estimate, we would have 5.6 / (2.2 * 10-4) = 26,000 individual D. pulex. (back)