Summary
Haller’s Rule states that smaller animals have more brain mass per unit body mass than bigger animals. Because this observation seems to apply quite generally, it's helpful in calculations of wild-animal suffering as a function of fauna biomass.
Contents
Introduction
It's plausible that the sentience we attribute to an animal should, as a rough approximation, be an increasing function of its brain size. For example, if an animal has a brain of mass m, perhaps we think its sentience is proportional to mα for some α > 0, such as α = 0.5 or α = 1.
However, explicit numbers for an animal's brain size are generally harder to come by than numbers for an animal's overall mass. In ecology, raw biomass tends to be a more common unit to work with, especially when thinking about energy flow in food webs. So it would be helpful to have a quick conversion from an animal's overall body mass M to its brain mass m.
Haller’s Rule
This article explains:
A long history of studies of vertebrate animals has demonstrated that the relationship between brain and body mass follows a power-law function. Smaller individuals have relatively larger brains for their body sizes. This scaling relationship was popularized as Haller’s Rule by German evolutionary biologist Bernhard Rensch in 1948, in honor of Albrecht von Haller, who first noticed the relationship nearly 250 years ago. Little has been known, however, about relative brain size for invertebrates such as insects, spiders and nematodes, even though they are among Earth’s more diverse and abundant animal groups. But a recent wave of studies of invertebrates confirms that Haller’s Rule applies to them as well, and that it extends to much smaller body sizes than previously thought.
In particular, Haller's Rule postulates that brain mass m is a function of body mass M of the form m ∝ Mb for some coefficient b, such as b = 2/3. That equation implies that ln(m) = a + b * ln(M).
This paper says:
This allometric relationship between body and brain size has been documented extensively for vertebrates [Cuvier, 1845; Harvey and Krebs, 1990; Hanken and Wake, 1993; Striedter, 2005; Gonzalez-Voyer et al., 2009]. In contrast, relatively little is known about brain allometry for the numerous invertebrate taxa with extremely small body sizes, such as tardigrades [Zantke et al., 2008] or Arthropoda (insects, mites and spiders) [see also Rensch, 1948; Cole, 1985]. [...] The most extensive allometric study on invertebrate brains presented data from 10 ant species, albeit with limited taxon sampling [...] [Wehner et al., 2007]. That study demonstrated that the allometric scaling component for ants (b = 0.57) was similar to that for birds (b = 0.58) and reptiles (b = 0.54) but significantly different from that of mammals (b = 0.77).
The paper found the following results for ants:
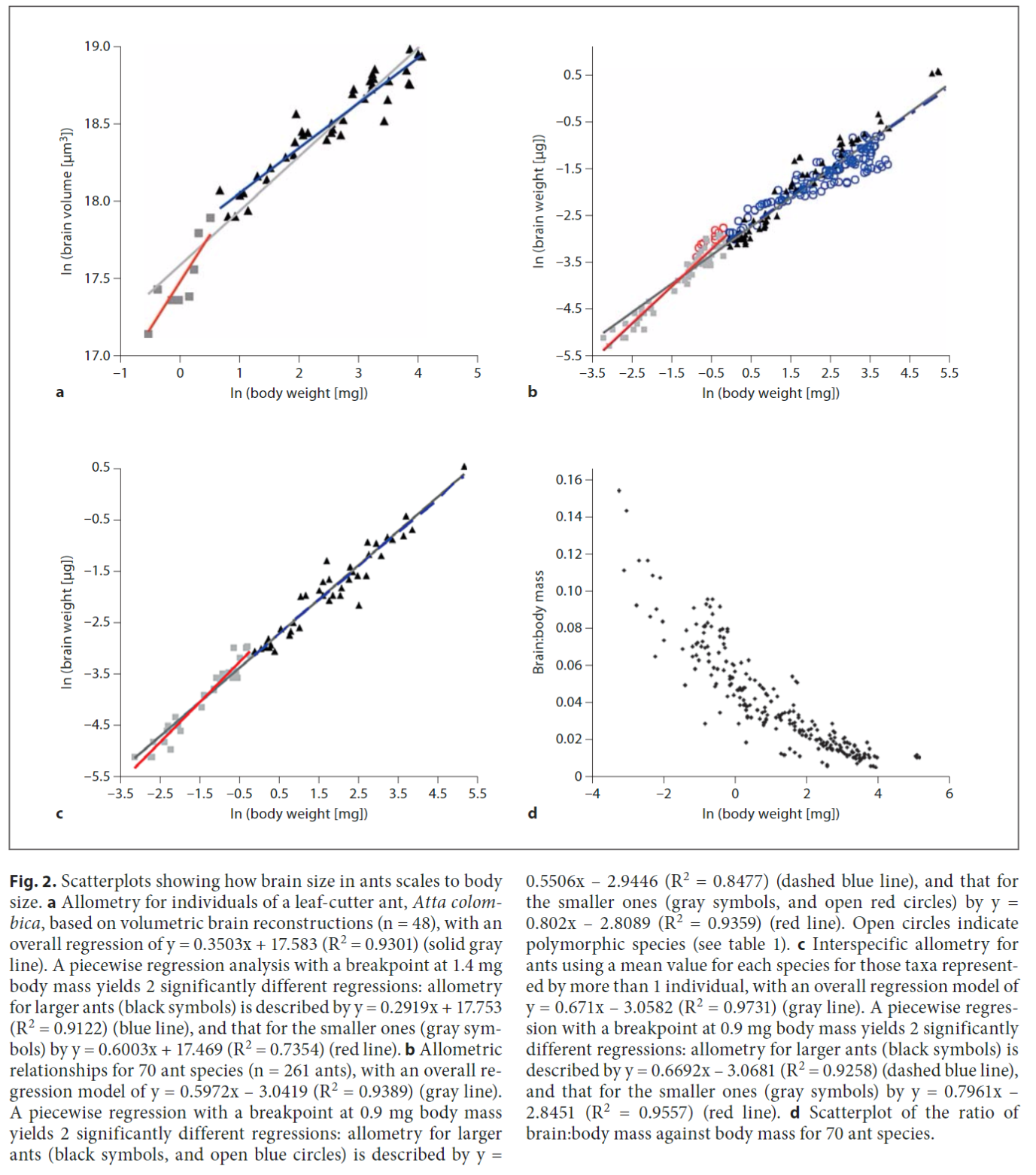
You can also see the trend for smaller animals to have higher brain-to-body-mass ratios in the table here.
The following figure is taken from this paper and based on this book (it uses a little m to denote body size, whereas I use a big M):
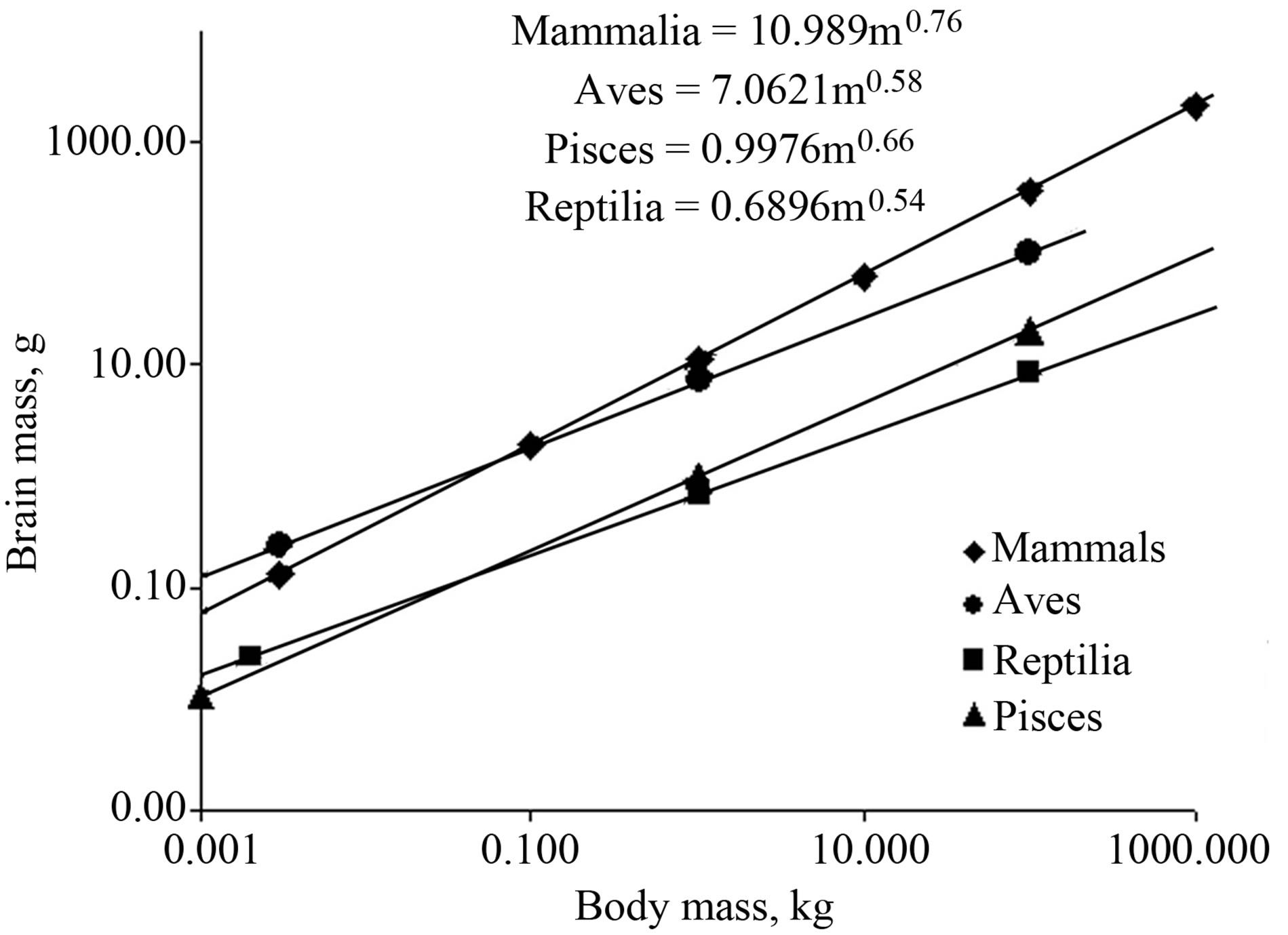
The exponents in the above graph seem to be around 1/2 to 3/4. In general, allometricians suggest the exponent of the curve relating body size to brain size is roughly 2/3 or 3/4 across animals.
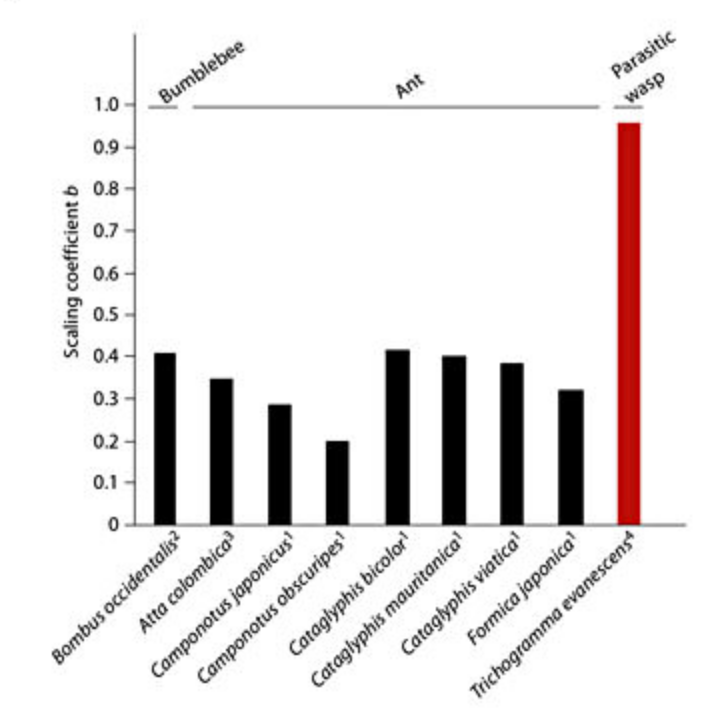
This paper reports on an exception to Haller's Rule for parasitic wasps:
Implications
Smaller animals may matter more per gram
If you think an animal's sentience is strictly proportional to its brain mass, then Haller's Rule suggests that in general, sentience scales less than linearly in body mass.
Suppose that m = c * Mb for some constant c. And suppose you think that the sentience of a brain of mass m is proportional to mα for some α. Then the sentience of an animal of body mass M is proportional to (c * Mb)α ∝ Mα b.
One implication of this is that as long as α < 1/b, then a given biomass of animals will contain more total sentience (and hence plausibly more total suffering) if it's composed of lots of small animals rather than a few big animals. In particular, suppose we have a total biomass of B, divided among N equally sized animals. Each animal has mass B/N. Total sentience is proportional to the number of animals, N, times the sentience per animal, (B/N)α b. Ignoring the B factor, that's proportional to N / Nα b, which increases as N increases (i.e., as the animals get smaller) if α b < 1.
Body metabolism vs. brain size
Kleiber's law suggests that an organism's metabolic activity scales roughly as M3/4.
If we assume that the Haller's Rule coefficient b is also 3/4 (which is approximately true for mammals), then the ratio of brain size to metabolic activity would be proportional to M3/4 / M3/4 = 1, i.e., roughly constant regardless of body size. In other words, the number of gram-years of brain mass that could be supported by a given number of Joules of metabolic energy would be constant. This suggests that if you have a given amount of food energy, it would support roughly the same number of gram-years of animal brain mass whether it was fed to a mouse or a cow.
To see this, suppose that an animal with metabolic rate R Joules per year has brain of mass m kg. R and m are both proportional to M3/4. Given some input amount of food of F Joules, it would be eaten in F/R years, and it would support a brain mass of m kg during those years (assuming for simplicity that the animal isn't growing during this time).a So the kg-years of brain tissue supported would be m * F/R. Since m and R are both proportional to M3/4, m * F/R is independent of M. Thus, the kg-years of brain supported is constant regardless of how the input feed is partitioned among animals of different sizes or among the growth stages of a given animal.
Of course, that kg-years of brain tissue are constant doesn't mean suffering is, since smaller animals tend to experience many more painful deaths per unit time.
Brain metabolism vs. brain size
One potential measure of sentience is the number of Joules per second used by a brain, since more neurons firing more often use more energy. By Kleiber's law, an animal's metabolism scales as M3/4, and by Haller’s Rule, that animal's brain-to-body-mass ratio is m/M ∝ Mb/M. Assuming the fraction of an animal's total metabolism devoted to brain activity is proportional to the animal's brain-to-body-mass ratio, then the brain metabolic rate of the animal is proportional to M3/4 * Mb/M = Mb - 1/4. For example, if b = 3/4, brain metabolism would be proportional to M1/2.
Since m ∝ Mb, M ∝ m1/b, so that the animal's brain metabolism, Mb - 1/4, is proportional to (m1/b)(b - 1/4) = m1 - 1/(4b). This expression can approximate sentience as a function of brain size if one thinks sentience is just brain metabolism. For example, for b = 3/4, sentience as a function of brain size is proportional to m1 - 1/3 = m2/3. In general, the exponent of m will be less than 1 for any b > 0.
This article suggests that the ratio of brain metabolism to total body metabolism may be roughly constant. If that's true, then my assumption in the preceding two paragraphs that (brain metabolism)/(body metabolism) is proportional to (brain mass)/(body mass) would be incorrect.
Footnotes
- If the animal is growing, the argument may still work, because the different growth stages of the animal can be seen as different-sized animals. However, maybe this point fails because the growing animal needs extra food to incorporate into its tissues, whereas adult animals only need to maintain a constant size?? (back)