Summary
In a stylized model where an agent risks only death in order to achieve variable rewards at each time step, the agent will be more cautious at younger ages, because it has more potential future fitness to lose by dying early.
Setup
Consider an agent organism trying to maximize its expected future fitness. Fitness ultimately comes from bearing and possibly raising successful offspring, but let's also assign more intermediary "reward" values when the organism accomplishes something that helps it achieve it's final goal, e.g., gathering food, having sex with a good partner, saving its baby from a predator, etc. Denote the reward that an organism might accomplish at time t as rt. At each timestep, an organism is presented with a possible reward drawn from some probability distribution. It doesn't know what the potential reward for that time step will be until it gets there, although it does know the distribution from which they're drawn. In order to gain this reward, the organism may need to bear a risk. Suppose that the only risk is that the organism will die and lose its potential future rewards, with probability 1-pt. Thus, the organism successfully achieves its reward with probability pt. For simplicity, assume that pt has a constant value p at all times. At any given timestep, the organism can also choose not to seek the reward and thereby to avoid risk of death at that time.
If it doesn't die prematurely due to risk-taking, the organism has a maximum possible lifespan of L timesteps. At a given time t, the organism can imagine what it thinks its expected remaining fitness will be at a present or future time T. Denote this expected fitness by FT|t. In order to do this calculation, the organism will need to guess what its future rewards will be as well, since it only learns their actual values when the time comes. Denote the expected value of a reward at time T viewed from the standpoint of time t as rT|t. When T=t, the organism knows the actual value rt of the reward.
At each time t = 1, ..., L, the organism chooses to take the risk or not depending on which option gives a higher expected value of future fitness at that time, i.e.:
This says the organism will either wait it out until t+1 and just get an expected Ft+1|t from there onwards, or else it will take a risk now, and with probability p, it will gain a reward now, rt|t, and will also live to have expected future fitness Ft+1|t. With probability 1-p, the organism dies and has 0 future fitness.
Expected fitness calculations
FL+1|L = 0, because once you're dead, you have no more fitness. Then
FL|L = max[FL+1|L, p(rL|L + FL+1|L)] = max[0, p(rL|L + 0)] = prL|L.
In other words, in your last day of life, you have nothing to lose by dying, so you may as well take a risk for the reward.
What if you're at t=L-1 looking forward to t=L? It's certain that you'll take the risk when you get to t=L, so the max operation will always pick out the second argument:
FL|L-1 = p(rL|L-1 + FL+1|L-1) = prL|L-1.
The only difference from what we had before is that we need to use an expected value for the reward, rL|L-1, because we don't yet know the actual value, rL|L.
Next:
FL-1|L-1 = max[FL|L-1, p(rL-1|L-1 + FL|L-1)] = max[prL|L-1, p(rL-1|L-1 + prL|L-1)].
In this time step, the decision of whether to take a risk for the reward rL-1|L-1 depends on whether
p(rL-1|L-1 + prL|L-1) > prL|L-1, or
rL-1|L-1 > (1-p)rL|L-1.
I so far haven't specified the known distribution from which rewards are sampled, but I now need to in order to make things tractable from this point forward. Assume that rewards are uniform on the unit interval [0,1]. The expected value is thus 1/2, which means that ra|b = 1/2 for any a > b, because until the time of the reward comes, you can only guess what it will be.
Now the condition for taking a risk becomes
rL-1|L-1 > (1-p)/2.
Next consider FL-1|L-2. We don't know what rL-1|L-1 will turn out to be, so we can't say whether we'll take that risk at t=L-1. However, we do know that we'll take the risk iff rL-1|L-1 > (1-p)/2, and since rL-1|L-2 is uniform on [0,1], this has probability 1-(1-p)/2 = (1+p)/2. Then
FL-1|L-2 = (chance choose to wait at t=L-1)(expected value if wait) + (chance choose to take a risk at t=L-1)(expected value if take the risk)
= [(1-p)/2]prL|L-2 + [(1+p)/2]p[(expected value of rL-1|L-1 given that you took the risk) + prL|L-2].
Here we can substitute rL|L-2=1/2. The expected value of rL-1|L-1 given that you took the risk, is the expected value of rL-1|L-1 given that rL-1|L-1 > (1-p)/2. Since rL-1|L-1 is uniform, this expected value is [1+(1-p)/2]/2 = (3-p)/4. Substituting in:
FL-1|L-2 = [(1-p)/2]p(1/2) + [(1+p)/2]p[(3-p)/4 + p(1/2)]
= (p-p2)/4 + (3p+4p2+p3)/8
= (5p+2p2+p3)/8.
Continuing on:
FL-2|L-2 = max[FL-1|L-2, p(rL-2|L-2 + FL-1|L-2)] = max[(5p+2p2+p3)/8, p(rL-2|L-2 + (5p+2p2+p3)/8)].
We take the risk iff
p(rL-2|L-2 + (5p+2p2+p3)/8) > (5p+2p2+p3)/8, or
rL-2|L-2 > (5+2p+p2)/8 - (5p+2p2+p3)/8, or
rL-2|L-2 > (5-3p-p2-p3)/8.
Then
FL-2|L-3 = (chance choose to wait at t=L-2)(expected value if wait) + (chance choose to take a risk at t=L-2)(expected value if take the risk)
= [(5-3p-p2-p3)/8][(5p+2p2+p3)/8] + [1-(5-3p-p2-p3)/8]p[(1+(5-3p-p2-p3)/8)/2 + (5p+2p2+p3)/8]
= 89p/128 + 25p2/64 + 31p3/128 + 3p4/32 + 7p5/128 + p6/64 + p7/128.
Summary so far
| Variable | Formula | Value if p=1 | Value if p=0.95 |
| FL|L-1 | p/2 | 1/2 | 0.475 |
| FL-1|L-2 | (5p+2p2+p3)/8 | 1 | 0.856 |
| FL-2|L-3 | 89p/128 + 25p2/64 + 31p3/128 + 3p4/32 + 7p5/128 + p6/64 + p7/128 | 3/2 | 1.225 |
We can see how, for p<1, the increase in expected reward is not completely linear as age increases. This is because as the organism gets older, it needs to become more cautious about taking risks—only doing so when there's a bigger potential reward that can justify the occasion.
Graphs
Our analytical formulas quickly became intractable, but the problem is actually easy to represent computationally. In an Excel workbook, I created a column of random [0,1] rewards and then backwards from the end of the organism's life applied equation (1) at each timestep.
The following graphs show runs each with a single column of random numbers.
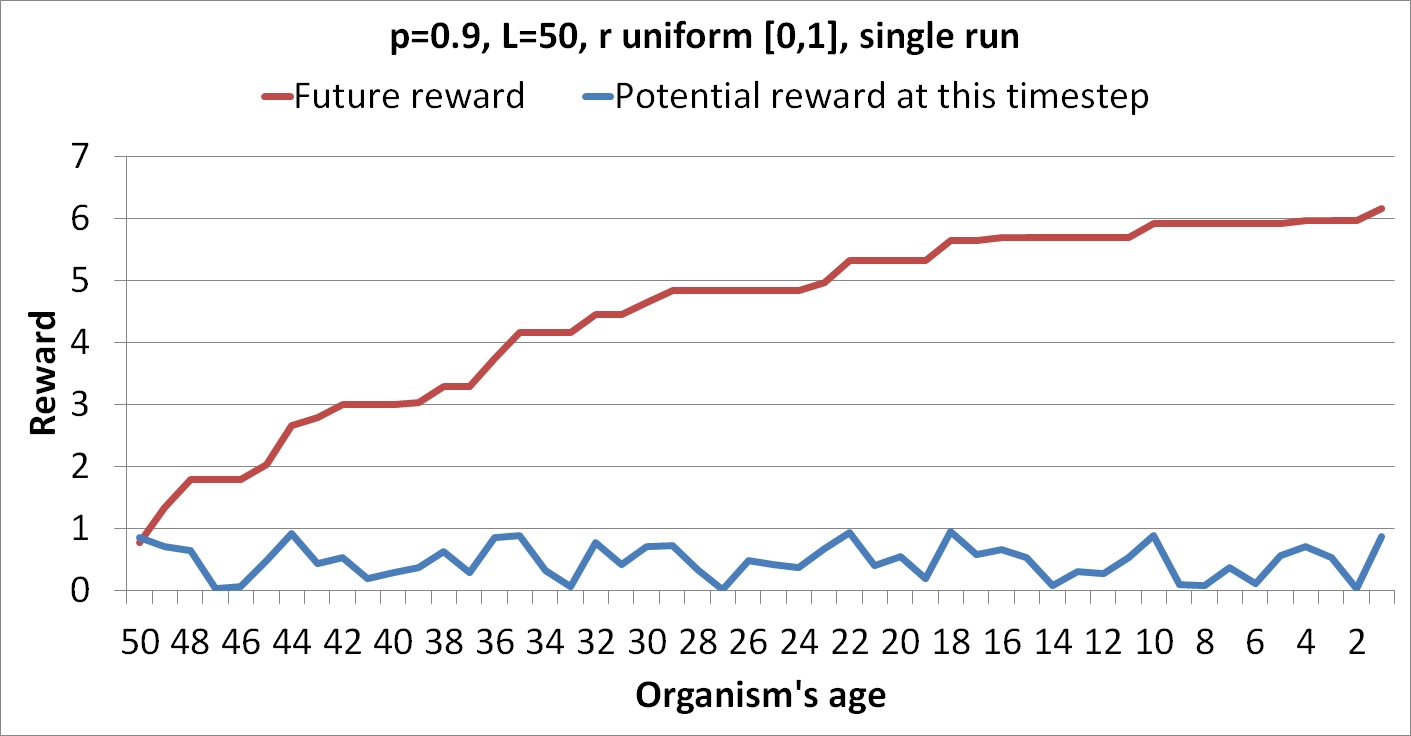
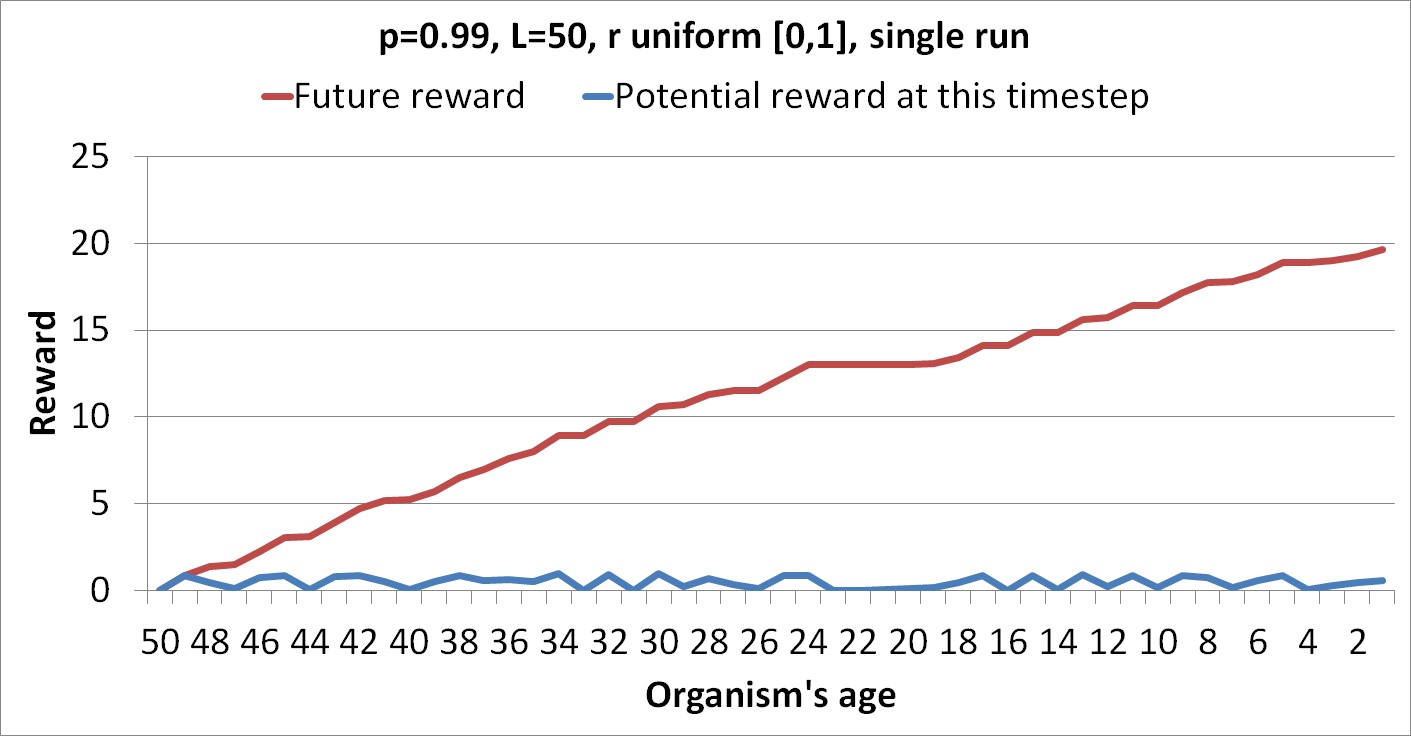
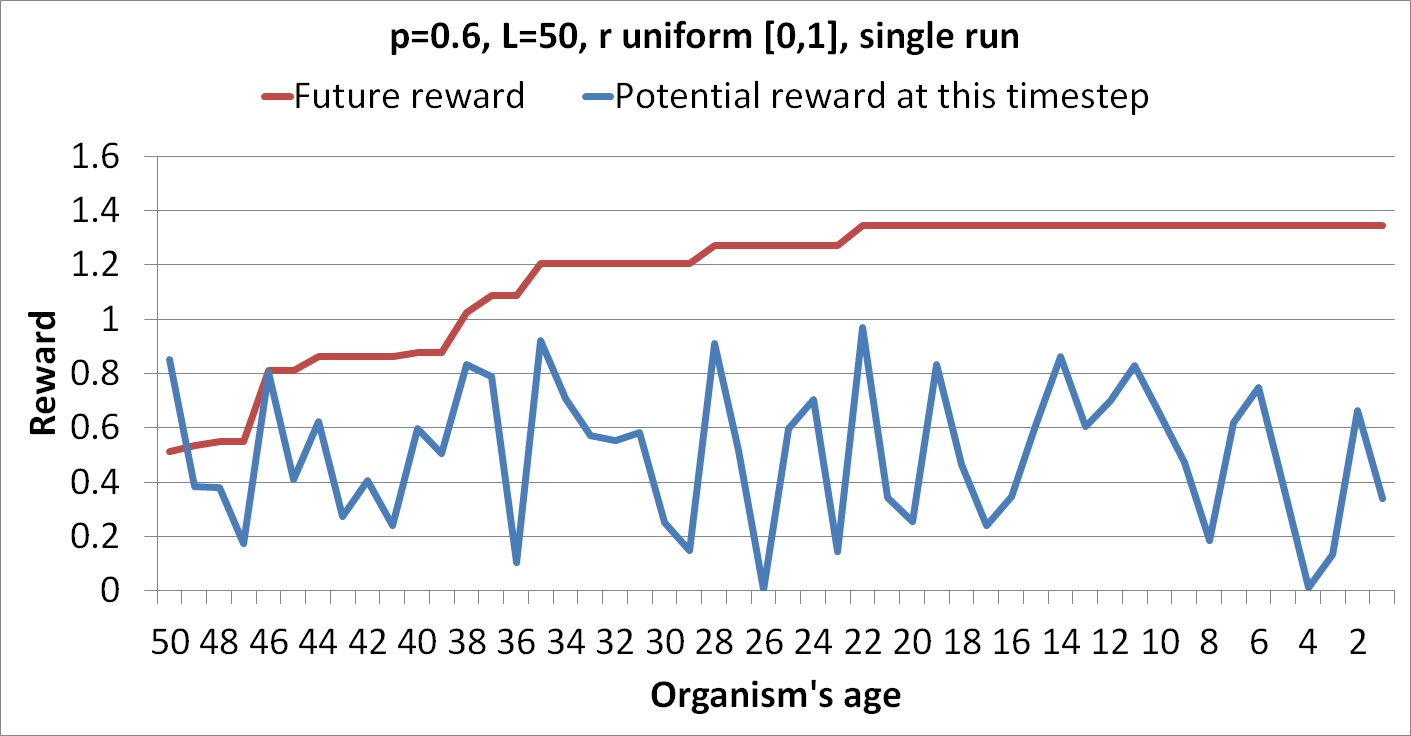
The flat regions are where the organism chooses not to take a risk because the reward at that point is too low.
These figures show only actual rewards for a particular run rather than expected rewards over all possible runs. The following graph shows an average of the future rewards over 10 different random columns.
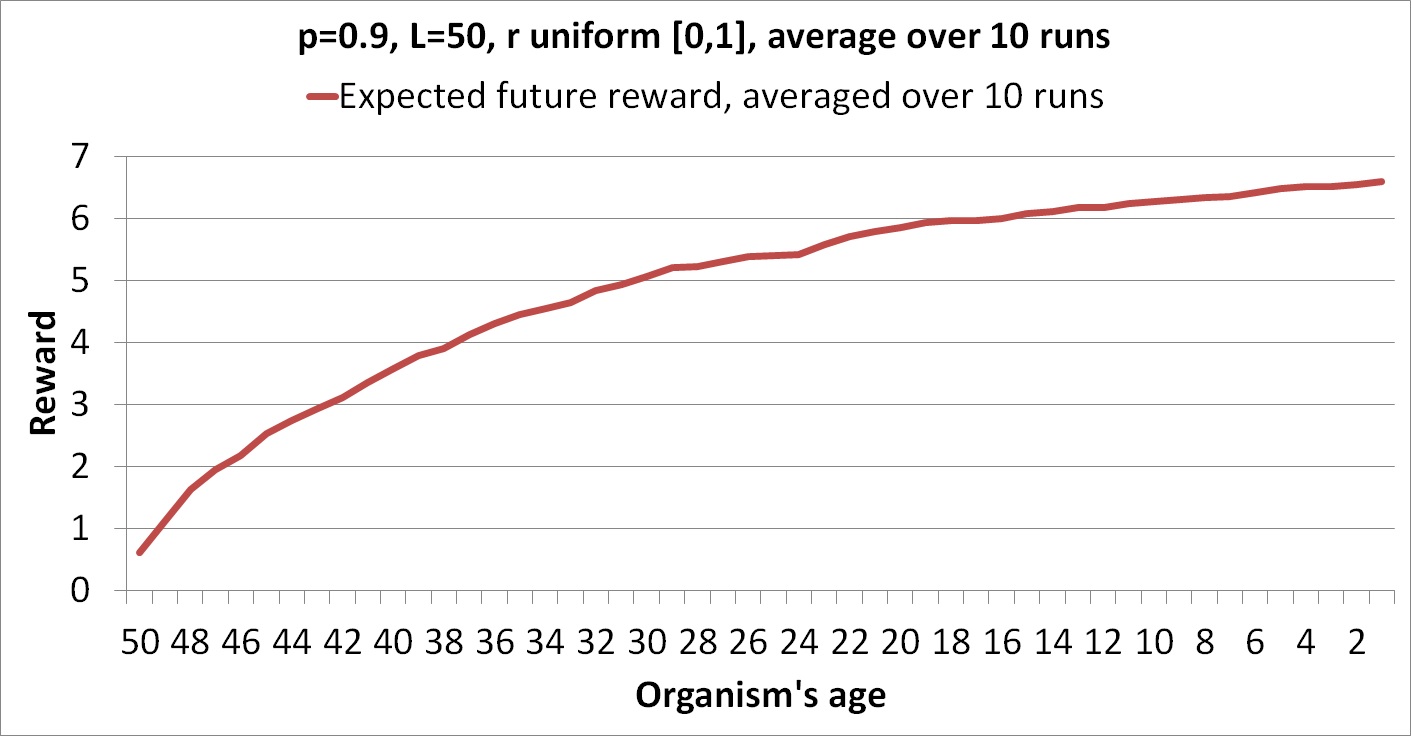
The graph is smoother because it shows expected values, but it's also noticeably concave because risk aversion grows as the organism has more potential future time ahead of it. In fact, we can establish an upper bound for how high the curve can get: p/(1-p). This is because if you had an indefinite potential lifespan L, the best you could do would be to wait until a reward of 1 came and then take the risk at that point. The expected value for the number of rewards you'd win before dying follows a geometric distribution and has mean p/(1-p).