Summary
This piece explores the question of whether one marine trophic level contains significantly more suffering than all others. For example, do zooplankton collectively matter much more or much less than fish? Answering this question could simplify analysis of the impacts of environmental policies on wild-animal suffering because attention could be focused on the most important trophic level(s). It turns out that if you estimate an animal's sentience as roughly proportional to its mass, then total suffering doesn't differ dramatically across trophic levels. If you think sentience as a function of mass is less than linear, then lower trophic levels will dominate—zooplankton or, if you don't think zooplankton matter at all, then the lowest level of fish. If you think sentience increases significantly faster than linearly with mass, then the highest trophic levels may dominate.
Contents
Introduction
It's difficult to evaluate the impacts of changes to marine ecosystems on wild-animal suffering. One factor that makes this hard is that marine food webs contain several layers of predation. In many cases, a reduction of animals at one trophic level implies an increase in populations at another trophic level, in line with the principle of trophic cascades.
Evaluating environmental policies would be easier if we could identify one or two marine trophic levels that contained the bulk of wild-animal suffering, since in that case, we could focus just on those trophic levels for the analysis. For example, suppose we concluded that zooplankton experienced significantly more aggregate suffering than their predators (forage fish). Then if a given ecological change decreased forage-fish populations by X% and increased zooplankton populations by X%, this change would be prima facie net bad because the zooplankton would matter more in total, so increasing their numbers would increase suffering more than reducing forage-fish numbers would reduce suffering.
Unfortunately, as I'll show in this piece, if you think the sentience of an animal is roughly linear in the animal's size, then total suffering among trophic levels looks somewhat uniform (at least within reasonable error margins), in which case simplifying the analysis to just one key trophic level may not be possible.
Sentience as a function of size
Most people have the intuition that not all animals count equally—e.g., a whale matters more than a copepod due to greater neural and cognitive complexity. Others think conscious animals all matter equally but maintain that copepods are very unlikely to be conscious. Either way, we need to describe the degree (or relative probability) of sentience of different organisms.
Ideally we would do this based on a number of factors, such as cognitive abilities, number of neurons, and complexity of cognitive algorithms. But such measures are hard to come by and to integrate into a single "sentience" number. As a crude approximation, we can describe the sentience s of an animal as a function of its brain mass m. In particular, I assume that s(m) ∝ mα for some constant α, typically in the interval [0,1] but possibly greater than 1. Assuming a roughly constant ratio r of brain mass to body mass among all organisms, the sentience of an organism of mass M would be s(m) = s(Mr) ∝ Mαrα ∝ Mα.
Is brain-to-body-mass ratio roughly constant?
In practice, brain-to-body-mass ratios are not constant: Brain mass scales less than linearly in body mass. One graph in this piece shows that for fish, it's approximately the case that m(M) = k M2/3 for some constant k. If we think that sentience s(m) = mα, then s(M) = (k M2/3)α = kα M2α/3 ∝ M2α/3. This would suggest somewhat more suffering at lower trophic levels than whatever you conclude from the main discussion in this piece.
For the sake of simplicity, I assume in the rest of this article that brain-to-body-mass ratios are constant across marine animals. Another reason to make this assumption is that I worry that a m(M) ∝ M2/3 relationship would give more weight to zooplankton than I'm comfortable with, given how simple they are. I probably give a single zooplankter less moral importance than a single insect of the same size because insects may be more intelligent. Plankton, being "drifters", may need less cognitive dexterity than land-based insects, though they do have neural machinery to jump away from predators.
However, if you want to account for the fact that smaller animals have bigger brain-to-body-mass ratios, you can just multiply by ~2/3 or something whatever α value you would have used for sentience as a function of brain mass.
Theoretical models based on energy transfer
"Fish abundance with no fishing: predictions based on macroecological theory" by Simon Jennings and Julia L. Blanchard presents a rough scaling law for the number density N of individuals of a fish species of mass M:
N(M) ∝ M(log10TE / log10PPMR) - 0.75,
where TE is transfer efficiency and PPMR is predator–prey body-mass ratio. The paper computes an estimated PPMR of 390, and it assumes TE values between 0.1 and 0.15. Let's assume TE = 0.15 in order to lean toward the side of overestimating the abundance of fish higher in the food chain. Then we have
N(M) ∝ M(log100.15 / log10390) - 0.75 = M-0.82/2.59 - 0.75 = M-1.07.
Then the aggregate sentience of organisms of mass M summed together would be proportional to s(M) N(M) = (Mα)(M-1.07) = Mα-1.07. For α ≤ 1, it seems as though smaller organisms lower on the food chain matter more in total, and for α around 0.5 or less, they matter much more. For example, consider three trophic levels: In the first, organisms have mass 1, in the next, they have mass 390 (i.e., the PPMR value), and in the third, 390*390 = 152,000. Then for α = 1, the aggregate sentience of the trophic levels would be proportional to the following numbers, respectively: 11-1.07 = 1, 3901-1.07 = 0.659, and 152,0001-1.07 = 0.434. The total sentience added over all trophic levels would be proportional to 1 + 0.659 + 0.434 = 2.093, so the percent of total sentience by trophic level would be 48%, 31%, and 21%, respectively. Doing the same calculation with α = 0.5 gives a distribution of aggregate sentience among the three trophic levels of 97%, 3%, and 0.1%, respectively.
Specific biomass estimates by another paper
Using some similar theoretical equations as those above, combined with estimates of worldwide primary production, the paper "Global-scale predictions of community and ecosystem properties from simple ecological theory" computed the following distribution of biomass by size class for marine animals globally:
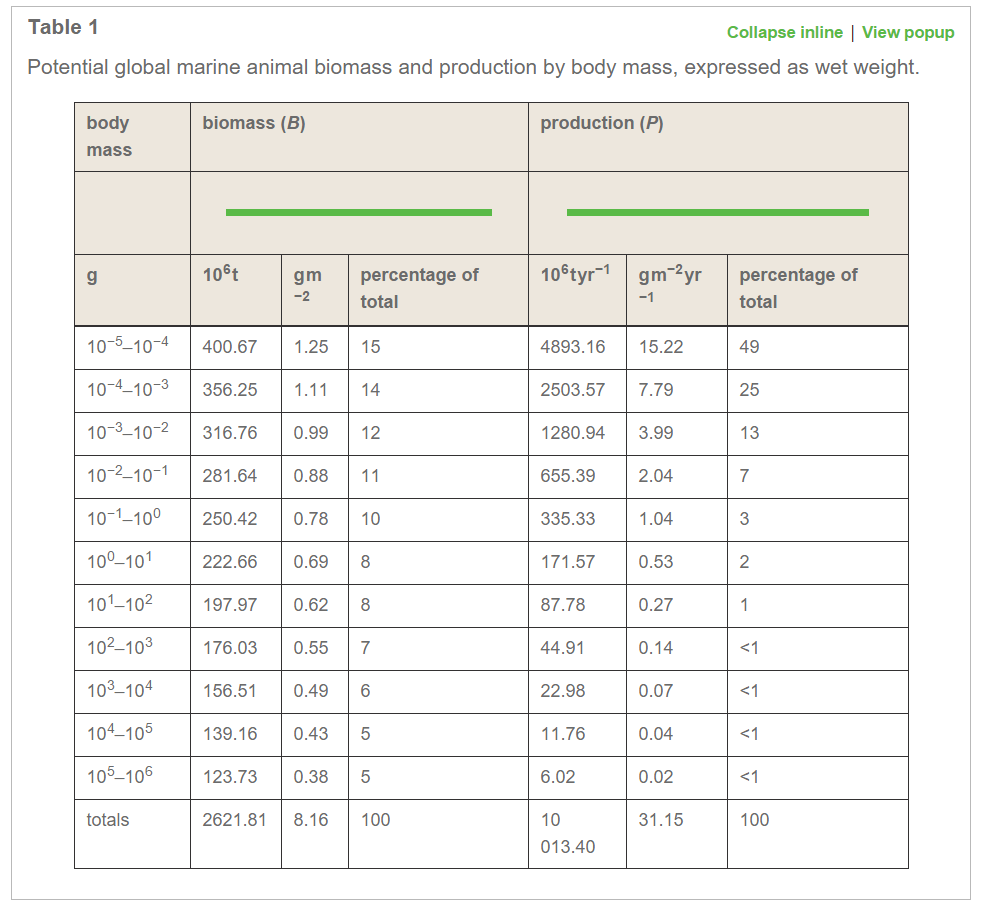
The results are quite similar as the equation above that N(M) ∝ M-1.07. To see this, remember that the total biomass B(M) as a function of M is M * N(M), which implies that we expect a curve roughly like B(M) ∝ M-0.07. And in fact, when I used a least-squares fit to estimate the exponent γ of the equation B(M) = (constant) * Mγ based on the above table, I found γ = -0.05. This isn't too surprising, because the data in the above table were computed based on theoretical equations, not based on actual measurements of global fish biomass by trophic level.
Biomass is roughly constant across trophic levels
This paper explains (p. 567) that it's common to model N(M) as being proportional to M-1 + λ, and
For stable pelagic ecosystems across trophic levels (e.g., Sheldon et al. 1972, Rodriguez and Mullin 1986, Sprules and Munawar 1986, Gaedke 1992, Cohen et al. 2003, Quin˜ones et al. 2003), and to some degree also for soil food webs (Mulder et al. 2005), the pattern is particularly clear, with λ ≈ 0.
The paper proceeds to offer an account in terms of top-down control about why λ would be roughly 0, without relying on the usual allometric explanations.
Using an elaborate ecosystem simulation, the authors produced the following figure (p. 574):

The fit line in this figure was N(M) ∝ M-0.95, which is quite close to the N(M) ∝ M-1.07 relationship discussed previously, suggesting that this scaling law is relatively robust as a general rule, though of course there are many exceptions.
The authors note that their model was particularly appropriate for marine food webs (p. 570):
Empirical estimates for model parameters were used whenever possible, and model variables are expressed in physical units. This allows a quantitative comparison of macroecological model properties (e.g., biomass densities) with empirical data. If there was a choice, we preferred parameter values applicable to pelagic communities, because (1) for pelagic communities the empirical pattern of body-mass–abundance scaling is particularly clear; (2) due to their relatively high spatial homogeneity, they might be comparatively easy to model; and (3) in the present form the model favors primary producers of small body mass resembling phytoplankton [...].
Another paper explains (p. 1924):
Some work on aquatic systems has suggested that biomass distributions are essentially constant across logarithmic body size intervals (Sheldon et al. 1972, Kerr 1974), while others have documented a great deal of variability (e.g., Sprules 1980, Sprules and Munawar 1986, Strayer 1986). Sprules and Munaware (1986) found that in planktonic communities deviations from a constant biomass distribution could be related to differences in ecosystem productivity. Thus, equal biomass in successive size categories, which we call the equal biomass hypothesis below, can be considered a baseline against which observed distributions can be compared.
However, that paper (p. 1927) rejected "the equal biomass hypothesis for North American birds."
Crude empirical estimates
In this section, I try guesstimating masses and numbers of organisms at each trophic level by stitching together some specific point estimates. I begin by presenting the results tables and then explain where the numbers came from.
Input tables and results
Sentience per individual = * (organism mass)^ +
| Trophic level | Body mass (g) | Sentience per individual |
| Big fish, predatory whales, etc. | ||
| Medium fish | ||
| Small fish | ||
| Bigger zooplankton | ||
| Smaller zooplankton |
| Trophic level | Number of individuals | * | Sentience per individual (set in previous table) | * | Badness of an individual's life + death per year | = | Total suffering at this trophic level per year | |
| Big fish, predatory whales, etc. | : | * 10^ | * | * | = | |||
| Medium fish | : | * 10^ | * | * | = | |||
| Small fish | : | * 10^ | * | * | = | |||
| Bigger zooplankton | : | * 10^ | * | * | = | |||
| Smaller zooplankton | : | * 10^ | * | * | = |
You might think that zooplankton are too simple to matter and only fish can meaningfully suffer. If so, feel free to ignore the zooplankton rows of the table. I'm personally undecided how much I care about zooplankton.
Badness per individual
The column "Badness of an individual's life + death per year" in the table above is based on calculations here, where I estimated that, using default parameters, the suffering per year per member of the not-just-hatched population was something like -200 for zooplankton and -10 for windowpane fish. Based on these estimates, I've added some made-up guesses into that column of the above table.
Page 15 of this paper has the following graphs showing how quickly marine organisms progress through tropic levels:
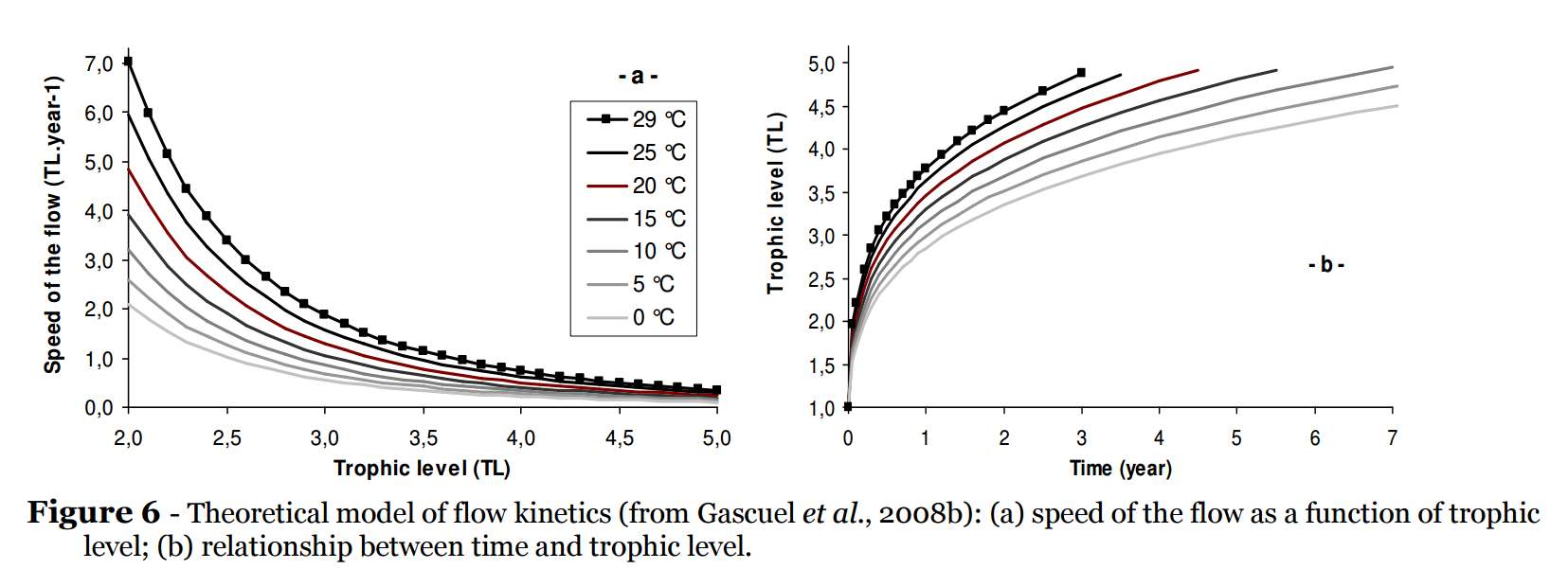
The right-hand graph shows that if the adult form of a species has a lower trophic level, it takes much less time to reach adulthood. Shorter lifespans by lower trophic-level animals mean more deaths per year, meaning more suffering per year.
Mass and numerosity estimates
Smaller zooplankton
It's estimated there are at least ~1018 zooplankton in the ocean and maybe as many as 1021. Let's say it's 1020.
How big are zooplankton? This study (figures 1 and 2) shows weights in the realm of 0.001 mg to 0.1 mg. Let's say 0.01 mg, or 10-5 g.
Multiplying this by 1020 gives a total zooplankton biomass of 1015 g.
Bigger zooplankton
Note that some zooplankton eat other zooplankton. For example, chaetognaths commonly eat copepods. So let's include a second trophic layer of zooplankton. One study reported that larger members of the species Sagitta enflata could eat "143.3 μg of prey dry weight" per day, which I'd guess is something like ~400 μg wet weight?a If the Sagitta enflata could eat this, it must have been several times bigger: perhaps a few milligrams? Since other Sagitta enflata are smaller, let's approximate the typical size as 1 mg, or 10-3 g.
Since, as we saw in the theoretical section above, total biomass is pretty constant among trophic levels, let's assume that these predator zooplankton have a total biomass on the same order of magnitude as prey zooplankton: 1015 g. Given a mass of 10-3 g per individual, this implies ~1018 individuals.
Small fish
One example predator of chaetognaths is Scophthalmus aquosus. This fish "Seldom exceeds weights of 350 to 400 g." Say a typical size is 200 g.
Global fish biomass has been estimated at 8.99 * 108 tons; approximate this as 109 tons, which is 1015 g. This is the same order of magnitude as the estimated zooplankton biomass above. If, unrealistically, all fish were 200-g Scophthalmus aquosus, there would be ~1013 fish.
Medium fish
A sample predator of Scophthalmus aquosus is the weakfish, which grows to 9 kg, or 9000 g. I don't have data on the global biomass of fish this size, but let's suppose it's the same as for previous trophic levels: 1015 g. Then if all these fish were 9000 g, there would be ~1011 of them.
Big fish, predatory whales, etc.
One predator of the weakfish is the dusky shark, which reaches 347 kg, or 3.5 * 105 g.
This study estimates that humans kill about ~100 million sharks per year, and the "current exploitation rates (herein defined as the total catch divided by the estimated biomass)" of sharks are between 6.4% and 7.9%. Say it's an exploitation rate of 7%. Then the number of sharks in the ocean should be at least (100 million)/0.07 = 1.4 * 109. Table 2 of that study shows average shark weights in the range of ~1 to ~100 kg (say 10 kg as a point estimate). That's a similar size as the Scophthalmus aquosus and smaller than the dusky shark. So probably the number of big sharks is a bit fewer.
In particular, if we suppose that the total biomass of sharks and other big predators ~105 g in size is 1014 g (a number consistent with the theoretical table above and one order of magnitude less than the 1015 g assumed for all previous trophic levels), then we'd have 109 big predators.
Footnotes
- Humans are ~60% water by mass, which suggests a conversion factor from dry mass to wet mass of about 1/0.4 = 2.5. Also, in this table, wet biomass tends to be a bit more than 3 times dry biomass. (back)